Distance from a point to a plane

The distance between a point in 3D space and a plane can be determined using vectors and trigonometry. This is handy in many situations, like making sure components are specific distances from certain planes in construction, determining distances between a airplane and a mountain or building in safe flight planning, and analysing how far away you need to place a light source or camera from a surface to create realistic shading. Use this resource to learn more.

In the figure, the blue plane extends in all directions. Points \(P_{1}\) and \(P_{2}\) lie on the plane. Point \(A\) is a point in the 3D space that does not lie on the plane.

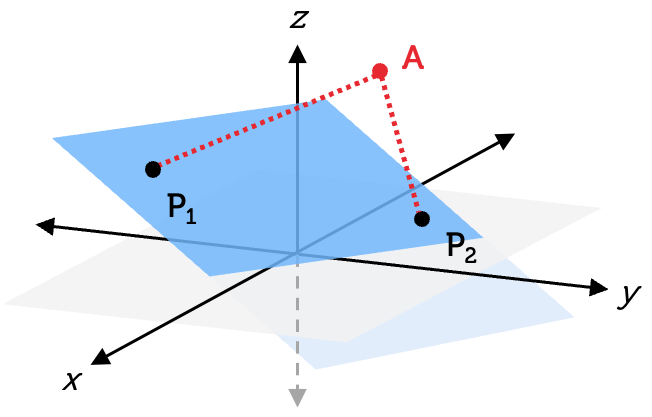
We can have any number of distances from a point \(A\) to the blue plane. For example, the distance from point \(A\) to point \(P_{1}\) is one possible answer. The distance from point \(A\) to point \(P_{2}\) is another.

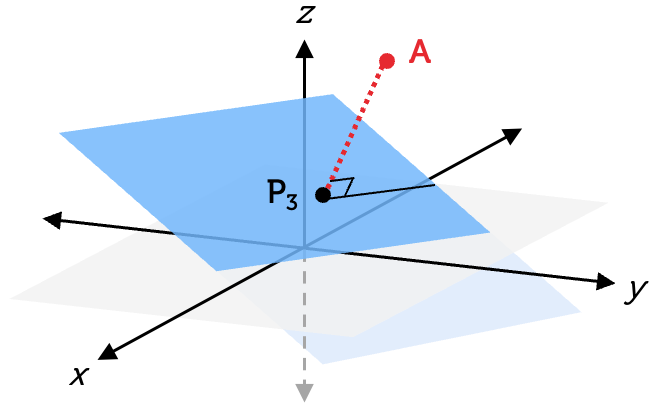
But when you are asked to find the distance between a point and a plane, you must provide the shortest distance. This is found by drawing a line at a right angle to the plane. Hence, the distance is also called the perpendicular distance between the point and the plane.

In this example, it would be the distance between point \(A\) and \(P_{3}\) in the following diagram.

Perpendicular distance

Consider the following figure.

To find the shortest distance from point \(A\) to the blue plane:

1. Choose any point \(P\) on the plane.
2. Define a vector from \(P\) to \(A\), \(\overrightarrow{PA}\).
3. Find the vector that is normal to \(\overrightarrow{PA}\).
4. Find a unit vector that is normal to the plane. This is sometimes called the unit normal or scalar resolute of \(\overrightarrow{PA}\) in the direction of \(\hat{n}\).
   

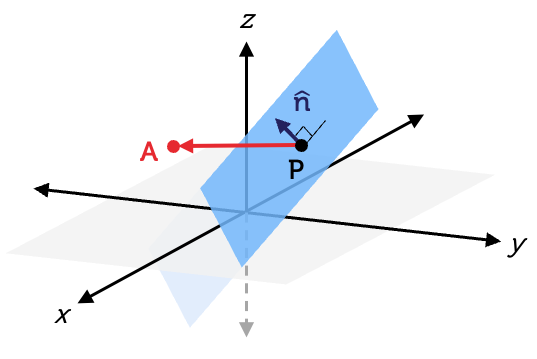
   \[\hat{n}=\frac{\vec{n}}{\left|\vec{n}\right|}\]

   Go back to review how to calculate magnitude of a vector if you need to.

5. Find the perpendicular distance using:
   

   \[\begin{align*} d & = \overrightarrow{PA}\cdot\hat{n}\\
   & = \overrightarrow{PA}\cdot\frac{\vec{n}}{\left|\vec{n}\right|}
   \end{align*}\]

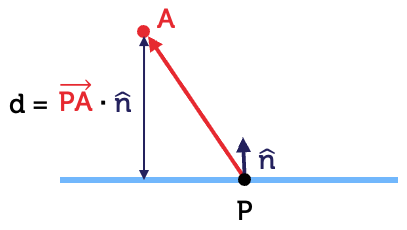
   This may be easier to understand if we rotate the figure so that we are looking at the blue plane from its edge.
   

   

Example – finding the distance between a point and a plane

Find the distance from the point \((2,5,4)\) to the plane \(x+2y+2z=2\).

Let point \(A=(2,5,4)\). We need to then find a point \(P\) on the plane. It can be any point but to make it easy, we can take \(y=z=0\).

Substituting in the equation for the plane, we get \(x=2\). So, the point on the plane is \(P=(2,0,0)\).

The vector from \(P\) to \(A\) is:
\[\begin{align*} \overrightarrow{PA} & =
(2-2)\hat{i}+(5-0)\hat{j}+(4-0)\hat{k}\\
& = 5\hat{j}+4\hat{k}
\end{align*}\]

Now, we need to find a unit vector that is normal to the plane. A normal vector is:
\[\vec{n} = \hat{i}+2\hat{j}+2\hat{k}\]

We can then find a unit normal vector:
\[\begin{align*} \hat{n} & = \frac{\vec{n}}{\left|\vec{n}\right|}\\
& = \frac{\hat{i}+2\hat{j}+2\hat{k}}{\sqrt{1^{2}+2^{2}+2^{2}}}\\
& = \frac{\hat{i}+2\hat{j}+2\hat{k}}{\sqrt{9}}\\
& = \frac{1}{3}\left(\hat{i}+2\hat{j}+2\hat{k}\right)
\end{align*}\]

Finally, we substitute the values into the formula to find the distance, \(d\).
\[\begin{align*} d & = \overrightarrow{PA}\cdot\hat{n}\\
& = \left(5\hat{j}+4\hat{k}\right)\cdot\frac{1}{3}\left(\hat{i}+2\hat{j}+2\hat{k}\right)\\
& = \frac{1}{3}\left(10+8\right)\\
& = 6
\end{align*}\]

Exercise – finding the distance between a point and a plane

1. Find the distance from the given point to the given plane.
1. \((0,0,0)\) and \(2x+3y-z=6\)
2. \((-1,1,2)\) and \(x+y=2\)
3. \((1,2,3)\) and \(3x+4y-z=1\)

Images on this page by RMIT, licensed under CC BY-NC 4.0