T9: Trigonometric identities

Trigonometric identities are equations involving trigonometric functions that are true for all values of the involved variables. They are essential tools for simplifying expressions and solving equations in mathematics. On this page, you'll learn about fundamental identities, double angle formulas, sums and difference, and other trigonometric functions.

An algebraic expression such as \(2x+7=5\) is an equation and it is
only true for one value of \(x\) (that is \(x=-1\)).

An expression such as
\[\begin{align*}
\tan x & =\frac{\sin x}{\cos x}
\end{align*}\]
however, is true for ALL values of \(x\). We call this an identity.

Trigonometric identities

To show that \(\tan x=\frac{\sin x}{\cos x}\) , you can recall that
in any right angled triangle, the sides of the triangle can be named.
The longest side is called the hypotenuse (abbreviated as \(Hyp\)),
we also have the side opposite a given angle (\(Opp\)) and the side
adjacent to the angle (\(Adj\)).

\(\sin\,\theta=\frac{\boldsymbol{O}pp}{\boldsymbol{H}yp}\)
\(\cos\,\theta=\frac{\boldsymbol{A}dj}{\boldsymbol{H}yp}\) \(\tan\,\theta=\frac{\boldsymbol{O}pp}{\boldsymbol{A}dj}\)

Therefore \(\dfrac{\sin\theta}{\cos\theta}=\dfrac{\frac{Opp}{Hyp}}{\frac{Adj}{Hyp}}=\frac{Opp}{Adj}=\tan\theta\)

Another identity, sometimes referred to as the fundamental trigonometric
identity, can be derived from the unit circle.

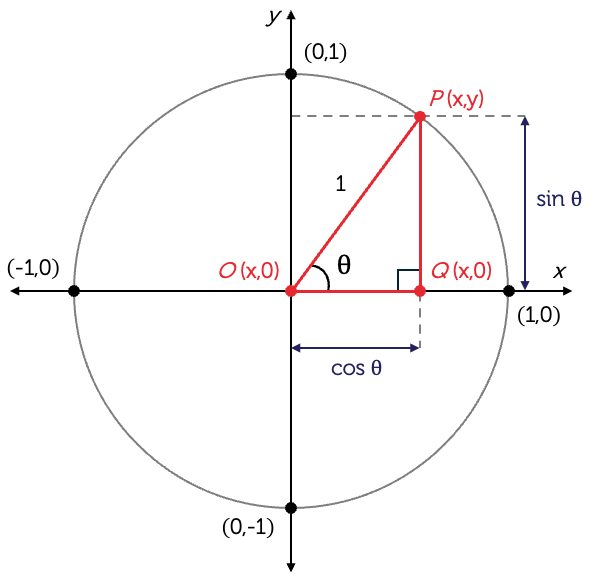
Applying Pythagoras’ theorem to the right angled triangle within the
unit circle we find that \(\left(\sin\theta\right)^{2}+\left(\cos\theta\right)^{2}=1^{2}\)
, that is:
\[\begin{align*}
\sin^{2}\theta+\cos^{2}\theta & =1.
\end{align*}\]
This is true for any value of \(\theta\).

Besides these two identities, there are many other trigonometric identities
that can be useful in simplifying or rearranging trigonometric expressions.

Fundamental identities

\[\begin{align*}
\tan\theta & =\frac{\sin\theta}{\cos\theta}\\
\sin^{2}\theta+\cos^{2}\theta & =1
\end{align*}\]

Double angle formulas

\[\begin{align*}
\sin2\theta & =2\sin\theta\cos\theta\\
\cos2\theta & =\cos^{2}\theta-\sin^{2}\theta\\
& =1-2\sin^{2}\theta\\
& =2\cos^{2}\theta-1\\
\tan2\theta & =\frac{2\tan\theta}{1-\tan^{2}\theta}
\end{align*}\]

Sums and differences

\[\begin{align*}
\sin(x+y) & =\sin x\cos y+\cos x\sin y\\
\sin(x-y) & =\sin x\cos y-\cos x\sin y\\
\cos(x+y) & =\cos x\cos y-\sin x\sin y\\
\cos(x-y) & =\cos x\cos y+\sin x\sin y\\
\tan(x+y) & =\frac{\tan x+\tan y}{1-\tan x\tan y}\\
\tan(x-y) & =\frac{\tan x-\tan y}{1+\tan x\tan y}
\end{align*}\]

Definitions of other trigonometric functions

There are also an number of definitions with which you should be familiar.
These are the definitions for cosecant (cosec or csc), secant (sec)
and cotangent (cot).

\[\begin{align*}
\csc x & =\frac{1}{\sin x}\\
\sec x & =\frac{1}{\cos x}\\
\cot x & =\frac{1}{\tan x}=\frac{\cos x}{\sin x}
\end{align*}\]

Examples

1. Simplify

1. \(\left(\tan x\right)\) \(\left(\cos x\right)\)

\[\begin{align*}
\left(\tan x\right)\left(\cos x\right) & =\frac{\sin x}{\cos x}\times\cos x\\
& =\sin x
\end{align*}\]

2. \(\sin x\cos x\left(\sin x+\frac{\sin2x}{2\tan x\sin x}\right)\)

\[\begin{align*}
\sin x\cos x\left(\sin x+\frac{\sin2x}{2\tan x\sin x}\right) & =\sin x\cos x\left(\sin x+\frac{2\sin x\cos x}{2\left(\frac{\sin x}{\cos x}\right)\sin x}\right)\\
& =\sin x\cos x\left(\sin x+\frac{\cos x}{\frac{\sin x}{\cos x}}\right)\\
& =\sin x\cos x\left(\sin x+\frac{\cos^{2}x}{\sin x}\right)\\
& =\sin^{2}x\cos x+\cos^{3}x\\
& =\cos x\left(\sin^{2}x+\cos^{2}x\right)\\
& =\cos x\left(1\right)\\
& =\cos x
\end{align*}\]

2. 1. Solve for \(x\), \(\cos2x-3\cos x+2=0\), for \(0\leq x\leq2\pi\)

\[\begin{align*}
\cos2x-3\cos x+2 & =0\\
2\cos^{2}x-1-3\cos x+2 & =0\text{$\quad$ (using the identity $\cos2x=2\cos^{2}x-1)$ }\\
2\cos^{2}x-3\cos x+1 & =0
\end{align*}\]

Let \(a=\cos x\)
\[\begin{align*}
2a^{2}-3a+1 & =0\\
\left(2a-1\right)\left(a-1\right) & =0\\
2a-1=0 & \textrm{ or }a-1=0\\
a=\frac{1}{2} & \textrm{ or }a=1
\end{align*}\]

Substituting \(\cos x\) back in place of \(a\)
\[\begin{align*}
\cos x=\frac{1}{2} & \textrm{ or }\cos x=1\\
x=\frac{\pi}{3},\textrm{ $\frac{5\pi}{3}$ } & \textrm{ or }x=0,2\pi\\
x & \textrm{ =$0,\frac{\pi}{3},\textrm{ $\frac{5\pi}{3}$ },2\pi$ }
\end{align*}\]

2. Solve \(\cos^{2}x-2\sin x+2=0\), for \(0\leq x\leq2\pi\) .

Given that
\[\begin{align*}
\sin^{2}x+\cos^{2}x & =1\\
\cos^{2}x & =1-\sin^{2}x.
\end{align*}\]

Therefore

\[\begin{align*}
\cos^{2}x-2\sin x+2 & =0
\end{align*}\]

can be written as
\[\begin{align*}
1-\sin^{2}x-2\sin x+2 & =0\\
-\sin^{2}x-2\sin x+3 & =0\\
\sin^{2}x+2\sin x-3 & =0.
\end{align*}\]

Let \(a=\sin x\)
\[\begin{align*}
a^{2}+2a-3 & =0\\
\left(a+3\right)\left(a-1\right) & =0\\
a+3=0 & \textrm{ or }a-1=0\\
a=-3 & \textrm{ or }a=1.
\end{align*}\]

Substituting \(\sin x\) back in place of \(a\)
\[\begin{align*}
\sin x=-3 & \textrm{ or }\sin x=1\\
\textrm{no solution} & \textrm{ or }x=\frac{\pi}{2}\\
x & \textrm{ =$\frac{\pi}{2}$ }
\end{align*}\]

3. Given that \(\sin\frac{\pi}{6}=\frac{1}{2}\) and \(\sin\frac{\pi}{4}=\frac{1}{\sqrt{2}}\) and that \(\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}\textrm{ and }\cos\frac{\pi}{4}=\frac{1}{\sqrt{2}}\), find the exact value of \(\sin\frac{5\pi}{12}\).

\[\begin{align*}
\sin\frac{5\pi}{12} & =\sin\left(\frac{3\pi}{12}+\frac{2\pi}{12}\right)\\
& =\sin\left(\frac{\pi}{4}+\frac{\pi}{6}\right)
\end{align*}\]

Using the identity \(\sin(x+y)=\sin x\cos y+\cos x\sin y\), we get

\[\begin{align*}
\sin\left(\frac{\pi}{4}+\frac{\pi}{6}\right) & =\sin\frac{\pi}{4}\cos\frac{\pi}{6}+\cos\frac{\pi}{4}\sin\frac{\pi}{6}\\
& =\frac{1}{\sqrt{2}}\times\frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}}\times\frac{1}{2}\\
& =\frac{\sqrt{3}}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}\\
& =\frac{\sqrt{3}+1}{2\sqrt{2}}
\end{align*}\]

Exercises

1. Show that \(\left(\sec x\right)\left(\cot x\right)=\csc x\)
2. Simplify
   \(\quad\)a) \(\dfrac{\sin2\theta}{\sin\theta}\)
   \(\quad\text{b) }\) \(\cos2\theta+2\sin^{2}\theta\)
3. Solve \(\sin^{2}x-\cos x-1=0\), for \(0\leq x\leq2\pi.\)
4. Given that \(\sin\frac{\pi}{3}=\frac{\sqrt{3}}{2}\), \(\sin\frac{\pi}{4}=\frac{1}{\sqrt{2}}\),
   \(\cos\frac{\pi}{3}=\frac{1}{2}\textrm{ and }\cos\frac{\pi}{4}=\frac{1}{\sqrt{2}}\)
   find the exact value of \(\sin\frac{\pi}{12}\).