Constructing an access ramp
Explore these skills in a real world context.
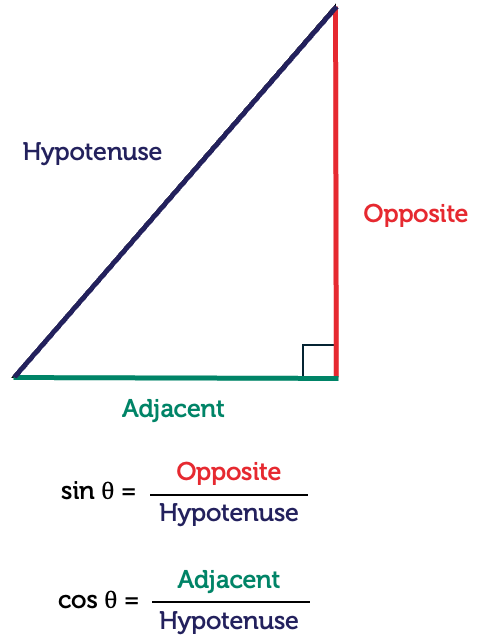
Explore the relationships between the angles and side lengths of a right-angled triangle. You will learn how to use trigonometric ratios to find unknown angles and lengths, enhancing your ability to solve geometric problems. Mastering this concept is vital for fields such as engineering, physics, and architecture, where precise calculations of angles and dimensions are essential.
Trigonometry is a branch of math involving the study of triangles. The ability to use and manipulate trigonometric functions is necessary in other branches of mathematics, including calculus, vectors and complex numbers.
You already learned that the longest side of a right-angled triangle is called the hypotenuse. The hypotenuse is always opposite to the right angle.
The other two sides are named in relation to another known angle (or an unknown angle under consideration).
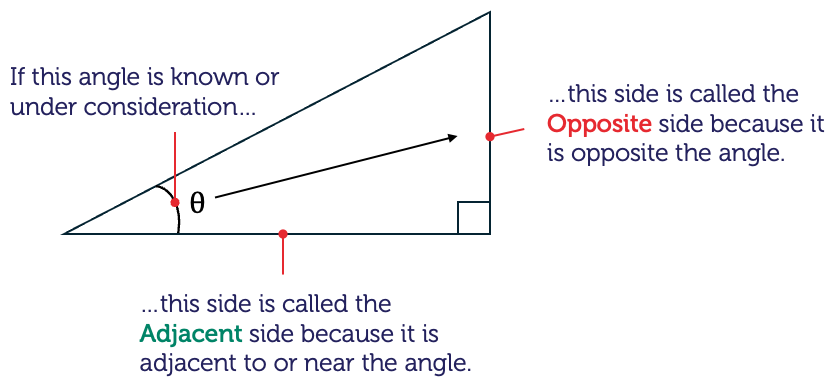
The angles and lengths of a right-angled triangle are related by three basic trigonometric ratios. In a right-angled triangle, the following ratios are defined for a given angle, \(\theta\):
\[\begin{align*} \textrm{sine}(\theta) & = \frac{\textrm{opposite length}}{\textrm{hypotenuse length}}\\
\textrm{cosine}(\theta) & = \frac{\textrm{adjacent length}}{\textrm{hypotenuse length}}\\
\textrm{tangent}(\theta) & = \frac{\textrm{opposite length}}{\textrm{adjacent length}}
\end{align*}\]
These ratios are abbreviated to \(\sin(\theta)\), \(\cos(\theta)\) and \(\tan(\theta)\), respectively.
A useful way to remember these relationships is using the mnemonic:
\[\textrm{SOH CAH TOA}\]
where
\[\sin(\theta) = \frac{\textrm{O}}{\textrm{H}}\quad\cos(\theta)=\frac{\textrm{A}}{\textrm{H}}\quad\tan(\theta)=\frac{\textrm{O}}{\textrm{A}}\]
In the right-angled triangle shown, evaluate \(\sin(\theta)\), \(\cos(\theta)\), and \(\tan(\theta)\).
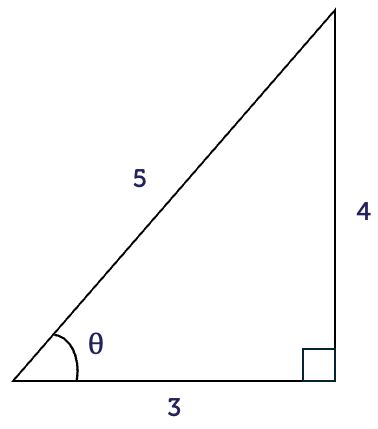
The first thing you should always do is name the sides of the triangle. The hypotenuse is the longest side with length \(5\). The opposite is the side opposite to the angle \(\theta\), with length \(4\). The adjacent is the side next to the angle \(\theta\), with length \(3\).
Then, we can use SOH CAH TOA to find \(\sin(\theta)\), \(\cos(\theta)\) and \(\tan(\theta)\).
\[\begin{align*} \sin(\theta) & = \frac{4}{5}\\
& = 0.8\\
\cos(\theta) & = \frac{3}{5}\\
& = 0.6\\
\tan(\theta) & = \frac{4}{3}\\
& \approx 1.33
\end{align*}\]
A right-angled triangle is shown.
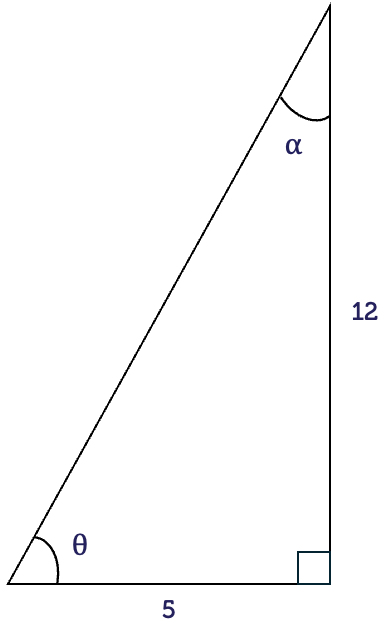
Hint: Use Pythagoras' theorem to find the hypotenuse.
Find the value of the angle \(\theta\) in the triangle shown.
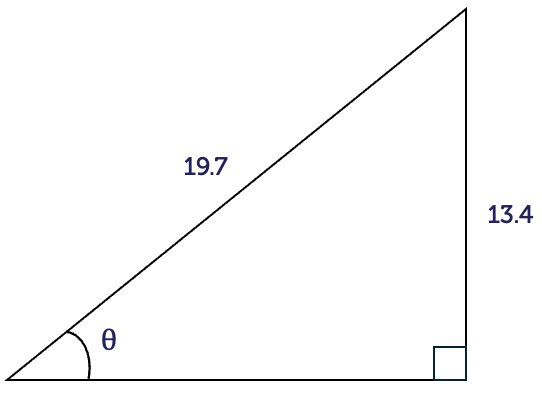
Name the sides of the triangle. The longest side is the hypotenuse with length \(19.7\). The side opposite to the angle \(\theta\) is the opposite with length \(13.4\). The side next to the angle is the adjacent with no length provided.
We have the lengths of the hypothenuse (H) and opposite (O), and the only relationship that connects the two is SOH or \(\sin(\theta)=\dfrac{\textrm{O}}{\textrm{H}}\).
\[\begin{align*} \sin(\theta) & = \frac{\textrm{O}}{\textrm{H}}\\
& = \frac{13.4}{19.7}\\
& = 0.6802
\end{align*}\]
To undo the \(\sin\) and find \(\theta\), we need to take the inverse \(\sin\), or \(\sin^{-1}\). You can do this on a scientific calculator.
\[\begin{align*} \sin\theta & = 0.6802\\
\theta & = \sin^{-1}(0.6802)\\
& = 42.9^{\circ}
\end{align*}\]
Don't forget to write the degree symbol!
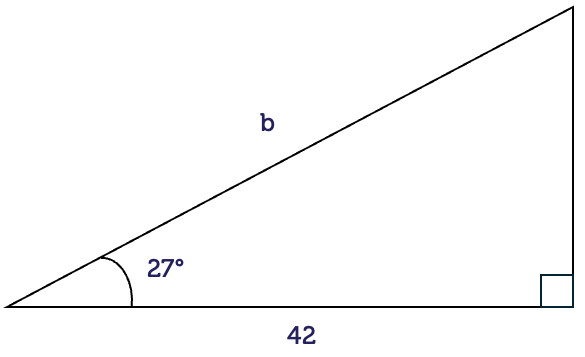
Find the unknown side length \(b\) in the following right-angled triangle.
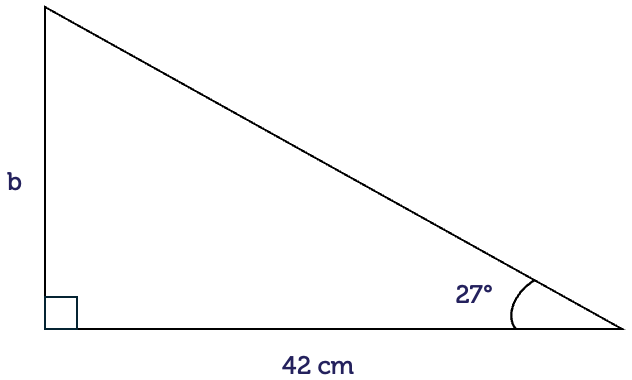
Here, we know an angle and the adjacent (A) side. The side length to be determined is the opposite (O) side. The ratio that relates these two sides is the tangent ratio.
\[\begin{align*} \tan(\theta) & = \frac{\textrm{O}}{\textrm{A}}\\
\tan(27^{\circ}) & = \frac{b}{42}\\
(\tan(27^{\circ}))\times42 & = b\\
b & = 21.4\textrm{ cm}
\end{align*}\]
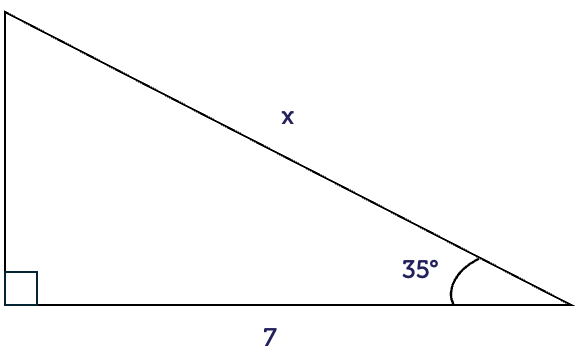
Here, we know an angle and the adjacent (A) side. The side length to be determined is the hypotenuse (H). The ratio that relates these two sides is the cosine ratio.
\[\begin{align*} \cos(\theta) & = \frac{\textrm{A}}{\textrm{H}}\\
\cos(35^{\circ}) & = \frac{7}{x}\\
(\cos(35^{\circ}))\times x & = 7\\
x & = \frac{7}{\cos(35^{\circ})}\\
x & = 8.55
\end{align*}\]
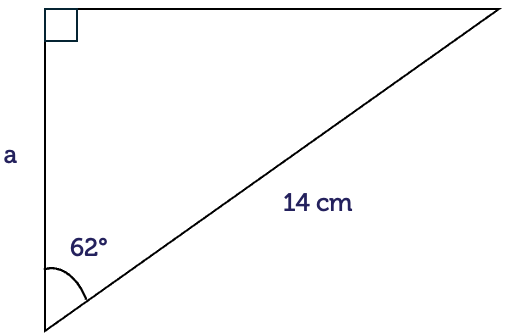
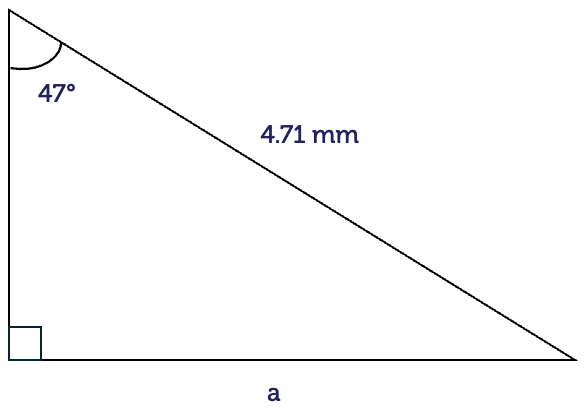
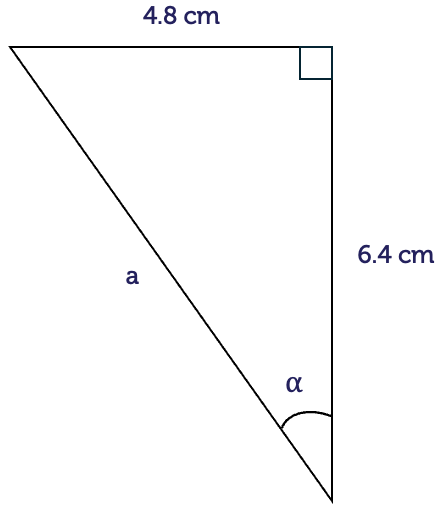
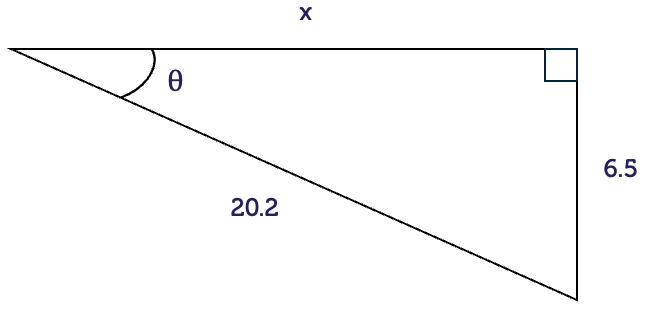
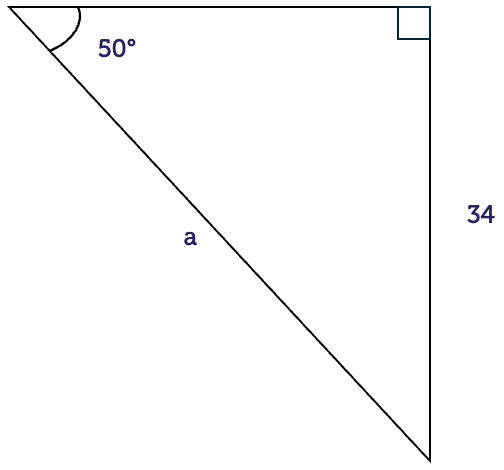
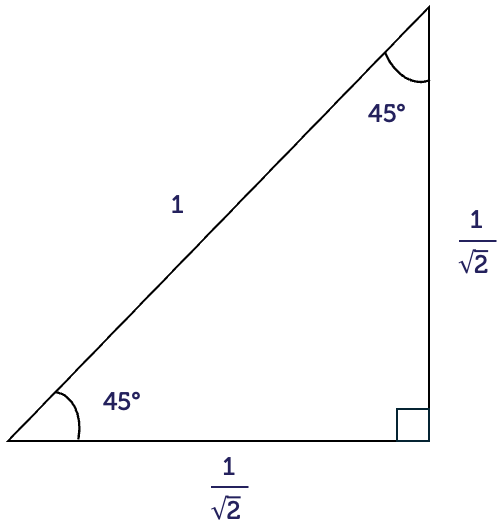
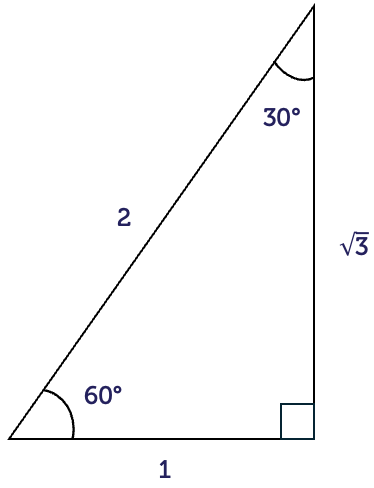
For right-angled triangles with special angles, the side lengths have exact values rather than decimal approximations. It is a good idea to remember these values. They occur often in maths courses.
First is the triangle with \(45^{\circ}\) angles.
Second is the triangle with angles \(30^{\circ}\) and \(60^{\circ}\).
Images on this page by RMIT, licensed under CC BY-NC 4.0