Circular functions
To solve trigonometric equations, it is critical to understand circular functions. Use this resource to refresh your understanding.
A calculator may only give you one answer to an inverse trigonometry question between \(0\) and \(90^{\circ}\). When you use the unit circle, you can visualise the many different solutions for the angle. Understanding this concept will help you in many STEM fields, such as satellite navigation in physics, and measurement of distances in architecture.
If you know the value of a trigonometric function, you can find all of the possible angles that satisfy this expression using the unit circle.
In circular functions:
For example, if the question is: Solve \(\cos(\theta)\) if \(-\pi \le \theta \le 3\pi\), then \(-\pi \le \theta \le 3\pi\) is the domain and the range would be the relevant solutions for \(\cos(\theta)\).
Solving these types of problems is easier if you can confidently identify the values of trigonometric functions on a unit circle. You also need to understand angles in degrees and radians. Go back and review circular functions and angle measurement before you proceed.
Given that \(\sin\theta=0.3\), find all values of \(\theta\) in the domain \(\left\{ \theta:0^{\circ}\leq\theta\leq360^{\circ}\right\}\).
First, sketch a unit circle and locate the points on the unit circle for which \(\sin(\theta)=0.3\)—that is, where \(y=0.3\).
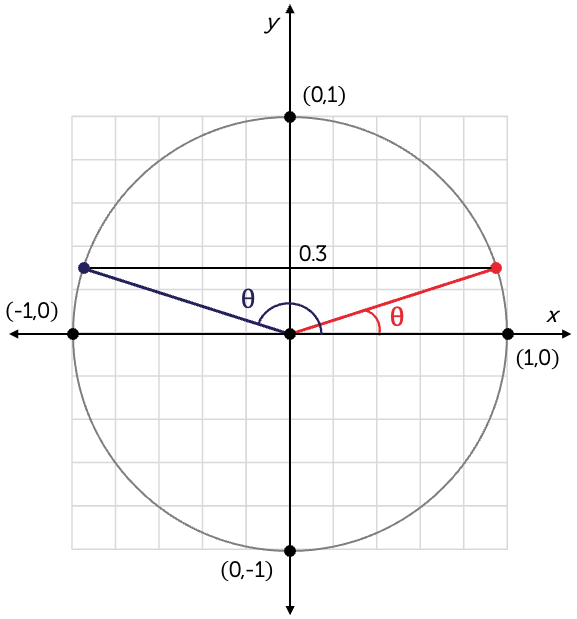
There are at least two solutions shown in red and blue. Let's call the red one \(\theta_{r}\) and the blue one \(\theta_{b}\).
\[\begin{align*} \theta_{r} & = \sin^{-1}\left(0.3\right)\\
& = 17.46^{\circ}\quad\textrm{from calculator}
\end{align*}\]
The other angle can be found by symmetry of the unit circle.
\[\begin{align*} \theta_{b} & = 180^{\circ}-\theta_{r}\\
& = 180^{\circ}-17.46^{\circ}\\
& = 162.54^{\circ}
\end{align*}\]
Hence, the solutions are \(\theta=17.46^{\circ}\) and \(162.54^{\circ}\).
You might notice that this is the same problem as in Example 1, but with the domain extended to \(500^{\circ}\).
In the same way, we can sketch a unit circle and locate the points for which \(\sin(\theta)=0.3\).

From Example 1, we know \(\theta=17.46^{\circ}\) or \(162.54^{\circ}\). If we add \(360^{\circ}\) to each of these, i.e. go around the unit circle a second time, they will still satisfy \(\sin\theta=0.3\) function. The question is, are they in the domain of interest?
\[\begin{align*} \theta & = 17.46^{\circ}+360^{\circ}\\
& = 377.46^{\circ}
\end{align*}\]
This is less than \(500^{\circ}\) and is therefore a solution to Example 2.
\[\begin{align*} \theta & = 162.54^{\circ}+360^{\circ}\\
& = 522.54^{\circ}
\end{align*}\]
This is greater than \(500^{\circ}\), and goes beyond the domain, so it is not a solution to Example 2.
Hence, the solutions are \(\theta=17.46^{\circ},\,162.54^{\circ}\) and \(377.46^{\circ}\).
Sketch a unit circle and locate the points on the unit circle for which \(\cos\alpha=0.5\)—that is, where \(x=0.5\).
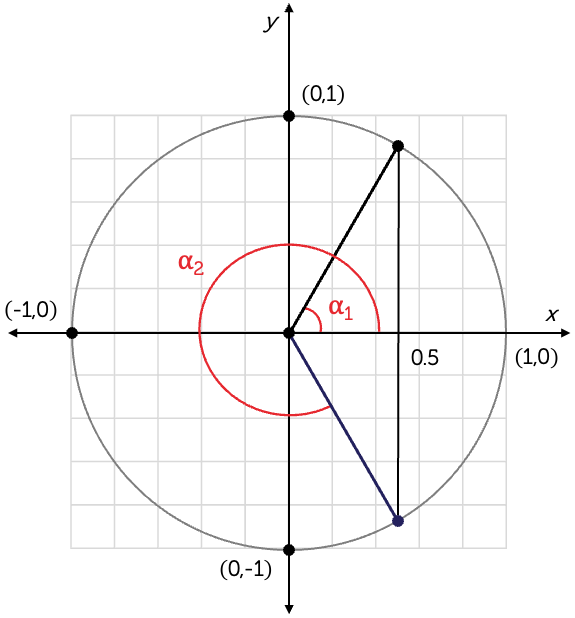
There are two possible solutions, \(\alpha_{1}\) and \(\alpha_{2}\).
\[\begin{align*} \alpha_{1} & = \cos^{-1}\left(0.5\right)\\
& = \frac{\pi}{3}\quad\textrm{from calculator}
\end{align*}\]
From symmetry of the unit circle:
\[\begin{align*} \alpha_{2} & = 2\pi-\alpha_{1}\\
& = 2\pi-\frac{\pi}{3}\\
& = \frac{5\pi}{3}
\end{align*}\]
Hence, the solutions are \(\alpha=\dfrac{\pi}{3}\) and \(\dfrac{5\pi}{3}\).
You might notice that this is the same problem as in Example 3, but with the domain extended to \(-2\pi\).
In the same way, we can sketch a unit circle and locate the points for which \(\cos(\alpha)=0.5\).
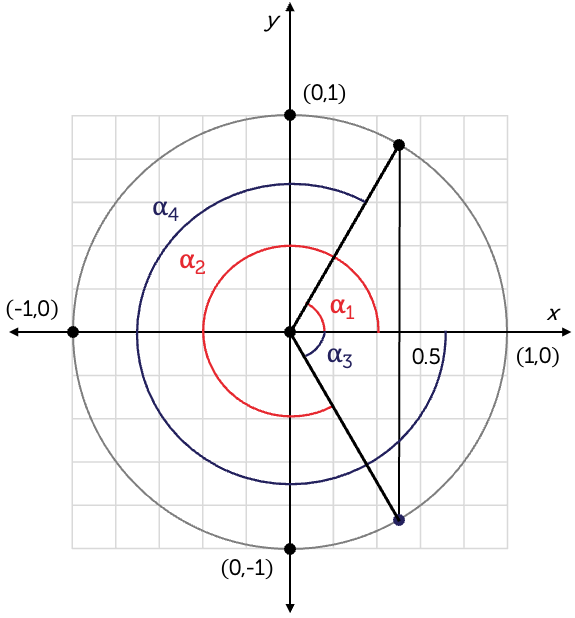
The two positive angles (shown in red) are the same as those in Example 3: \(\alpha_{1}=\dfrac{\pi}{3}\) and \(\alpha_{2}=\dfrac{5\pi}{3}\).
The negative angles (shown in blue) are \(\alpha_{3}\) and \(\alpha_{4}\).
Using the results from Example 3 and symmetry, we have:
\[\begin{align*} \alpha_{3} & = -\alpha_{1}\\
& = -\frac{\pi}{3}\\
\alpha_{4} & = -\left(2\pi-\alpha_{1}\right)\\
& = \alpha_{1}-2\pi\\
& = \frac{\pi}{3}-2\pi\\
& = -\frac{5\pi}{3}
\end{align*}\]
Hence, the solutions are \(\alpha=-\dfrac{5\pi}{3},\,-\dfrac{\pi}{3},\,\dfrac{\pi}{3}\) and \(\dfrac{5\pi}{3}\).
Since the variable is \(2x\), we have to redefine the domain to \(\left\{ 2x:-180^{\circ}\leq2x\leq360^{\circ}\right\}\).
Points for tangent functions can be a bit more difficult to locate on a unit circle at first, so what we can do is find the first angle using our calculator.
\[\begin{align*} \tan\left(2x\right) & = -3\\
2x & = \tan^{-1}\left(-3\right)\\
& = -71.57^{\circ}\quad\textrm{from calculator} \end{align*}\]
We can use this angle to draw a line that cuts through the origin \((0,0)\), then find the other angles that lie within \(-180^{\circ} \le 2x \le 360^{\circ}\).
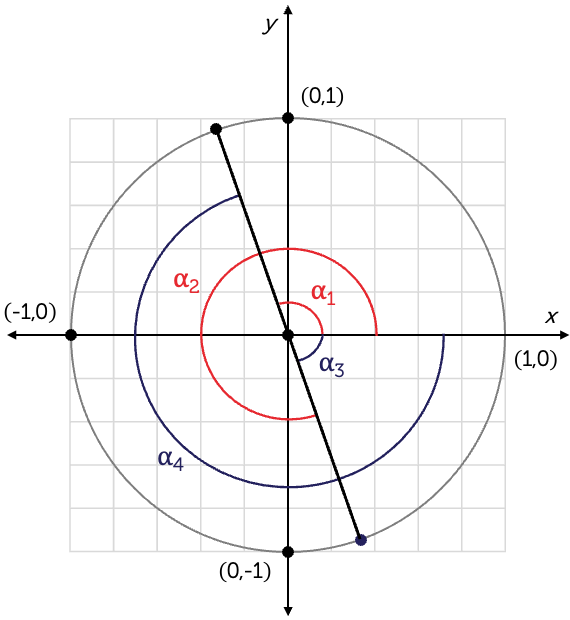
There are two positive angles \(\alpha_{1}\) and \(\alpha_{2}\) (shown in red) and two negative angles \(\alpha_{3,}\) and \(\alpha_{4}\) (shown in blue).
We can see that \(\alpha_{3}=-71.57^{\circ}\).
Using symmetry, we can find \(\alpha_{4}\).
\[\begin{align*} \alpha_{4} & = \alpha_{3}-180^{\circ}\\
& = -71.57^{\circ}-180^{\circ}\\
& = -251.57^{\circ}
\end{align*}\]
We can see that this is outside of the domain for \(2x\), so the answer is rejected.
Using the symmetry of the unit circle again, we can find \(\alpha_{1}\) and \(\alpha_{2}\).
\[\begin{align*} \alpha_{1} & = 360^{\circ}+\alpha_{4}\\
& = 360^{\circ}-251.57^{\circ}\\
& = 108.43^{\circ}\\
\alpha_{2} & = \alpha_{1}+180^{\circ}\\
& = 108.43^{\circ}+180^{\circ}\\
& = 288.43^{\circ}
\end{align*}\]
Hence:
\[\begin{align*} 2x & = \alpha_{3},\ \alpha_{1},\ \alpha_{2}\\
& = -71.57^{\circ},\ 108.43^{\circ},\ 288.43^{\circ}
\end{align*}\]
The solutions are \(x=-35.79^{\circ},\ 54.22^{\circ}\) and \(144.22^{\circ}\).
Solve for \(\phi\) in each of the following.
Images on this page by RMIT, licensed under CC BY-NC 4.0
Circular functions
To solve trigonometric equations, it is critical to understand circular functions. Use this resource to refresh your understanding.
Angular measurement and the unit circle
Angle measurement is important for solving trigonometric equations. Go back to this resource to brush up on your knowledge.