Skip to main content

Pythagoras’ theorem

Pythagoras’ theorem shows the relationship between the sides of a right-angled triangle. Knowing the length of two sides of a right-angled triangle, the length of the third side can be calculated. Understanding Pythagoras' theorem helps you solve problems in fields such as architecture, engineering, and computer graphs, where precise calculations of distances and lengths are crucial but can be difficult to physically measure.

Video tutorial – Pythagoras' theorem

Watch this video to learn how to use Pythagoras' theorem.

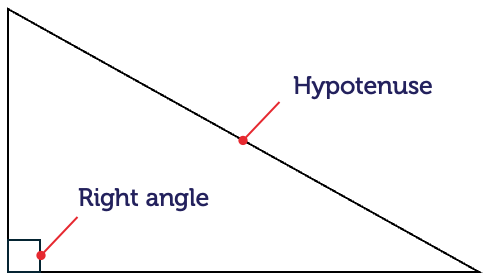
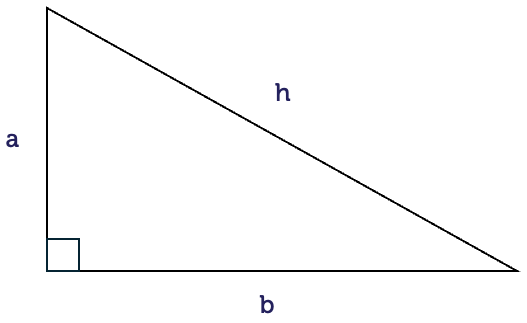
This is a short video on Pythagoras’ theorem. Let’s start with the definition of a right angled triangle first. It’s a triangle with one angle that’s 90 degrees, the longer side is opposite the right angle and is called the hypotenuse. Now let’s state Pythagoras’ theorem. It states that for any right angled triangle the square on the hypotenuse, h, is equal to the sum of the squares on the two shorter sides, a and b. In other words, h2 equals a2 plus b2.

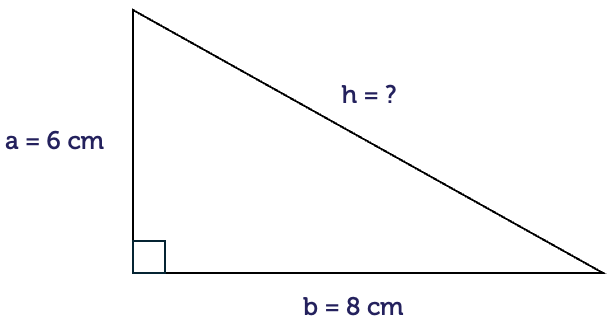
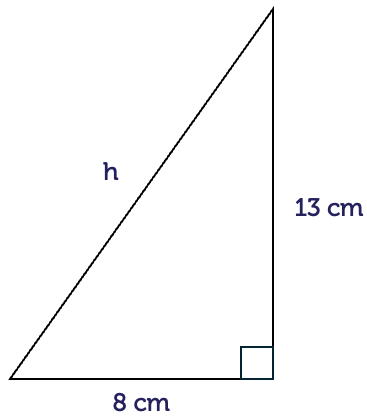
Let’s do an example. Let’s find the length of the hypotenuse of this particular triangle. We’re given the two shorter sides, a and b, so write the formula first a the top, h2 equals a2 plus b2 and substitute in for a and b, four and three. So we have 42 plus 32. Notice 42 is four times four, not four times two. So four time four is 16, 32 is three times three which is nine. So h2 equals 25. So if h2 is 25, then h is the square root of 25, which is five. In other words, the length of the hypotenuse is five.

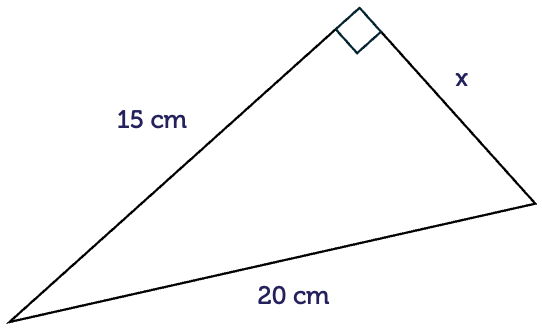
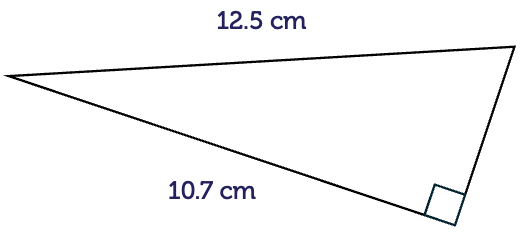
Now let’s find the length of one of the shorter sides of the triangle. Here we want to find the length of a. We’re given the hypotenuse. So as before we substitute into the formula, but notice I’ve turned the formula around this time and you’ll see why in a moment. In other words, I’ve got a2 plus b2 equals h2. Substituting b is six, h is 10, so a2 plus 36 equals 100. Now I want to remove 36 from the left hand side to isolate a. And that’s why I’ve turned the formula around this time, to make it easier, ‘cause I’m leaving a on the left hand side. So I’m subtracting 36, but remember we must subtract from both sides. So 36 minus 36 on the left hand side, 100 minus 36 on the right hand side. Therefore a2 equals 64, from which a is the square root of 64, which is eight. So the length of side a is 8.

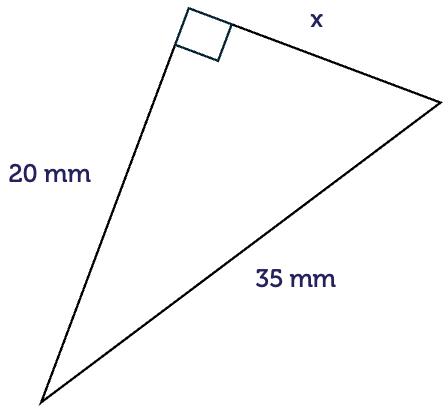
Now let’s look at the last triangle and we want to find the length of b, which is sometimes called the perpendicular side, because it’s at right angles to another side, in this case, a. a will be the horizontal line, b will be the perpendicular line, and the angle between the two will be 90 degrees. So substituting into the formula as before, we have a equals 24, and h is 25. The numbers are a bit larger but it still doesn’t change the method by which we’re doing the problem. So 242 plus b2 equals 252. 576 is 24 times 24, plus b2 equals 625, which is 25 times 25. And as before we remove the number from the left hand side to isolate the b. So we subtract 576 from the right hand side. 625 minus 576 gives us 49. If b2 equals 49 b is now the square root of 49 which is seven. In other words. The length of side b is seven.

Right-angled triangles

Triangles are plane shapes with three straight sides. A right-angled triangle contains an angle of \(90^{\circ}\), that is, a right angle.

A right angle is formed when two lines meet at an angle of \(90^{\circ}\). Usually, this is shown by two perpendicular lines.

A right-angled triangle with the hypotenuse labelled.

In a right-angled triangle, the longest side is opposite the right angle and is called the hypotenuse.

Pythagoras’ theorem

Pythagoras' theorem states that, in a right angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. This is represented by:

\[a^{2}+b^{2}=h^{2}\]
where \(h\) is the length of the hypotenuse, and \(a\) and \(b\) are the lengths of the other two sides.

A right-angled triangle with the sides labelled a, b and h for hypotenuse.

In some other resources, you may see that the hypotenuse is given the letter \(c\) instead of \(h\).

Pythagoras’ theorem does not apply to any triangle. It is only true for right-angled triangles.

Pythagoras’ theorem may be used to find the length of the third side of a triangle if you know the length of the other two sides.

Example 1 – using Pythagoras' theorem

Find the length of the hypotenuse in the triangle shown.

A right-angled triangle with the shorter sides equal to 6 and 8 centimetres respectively. The length of the hypotenuse is unknown.
\[\begin{align*} h^{2} & = a^{2}+b^{2}\\
& = 6^{2}+8^{2}\\
& = 36+64\\
& = 100\\
h & = \sqrt{100}\\
& = 10
\end{align*}\]

Don’t forget to include the unit of measurement in your answer! The length of the hypotenuse is \(10\textrm{ cm}\).

Find the length of the side \(x\) in the triangle shown to two decimal places.
A right-angled triangle with a hypotenuse of length 20 centimetres. One of the other sides is 15 centimetres long and the third side with an unknown length is labelled x.
\[\begin{align*} 20^{2} & = 15^{2}+x^{2}\\
x^{2} & = 20^{2}-15^{2}\\
& = 400-225\\
& = 175\\
x & = \sqrt{175}\\
& = 13.23
\end{align*}\]

The length of the side \(x\) is \(13.23\textrm{ m}\).

Find the length of the unknown side in the triangle shown to two decimal places.
A right-angled triangle with a hypotenuse of length 12.5 centimetres. One of the shorter sides is 10.7 centimetres. The last side length is unknown.
\[\begin{align*} 12.5^{2} & = 10.7^{2}+h^{2}\\
h^{2} & = 12.5^{2}-10.7^{2}\\
& = 156.25-114.49\\
& = 41.76\\
h & = \sqrt{41.76}\\
& = 6.46
\end{align*}\]

The length of the side is \(6.46\textrm{ cm}\).

Your turn – using Pythagoras' theorem

  1. Find the missing side length in the triangle.
    2. A right-angled triangle with the hypotenuse labelled as h and the other two sides of length 13 centimetres and 8 centimetres.
  2. Find the missing side length in the triangle.
    3. A right-angled triangle with hypotenuse 35 millimetres, another side 20 millimetres and the third side is labelled x.

  1. \(15.26\textrm{ cm}\)
  2. \(28.72\textrm{ mm}\)

Pythagorean triples

In some right-angled triangles, the lengths of all three sides are integers. When this occurs, the lengths are called a Pythagorean triple.

Some examples are \(\left(3,4,5\right)\), \(\left(5,12,13\right)\), \(\left(7,24,25\right)\) and \(\left(8,15,17\right)\). Multiples of these numbers are also Pythagorean triples.

Images on this page by RMIT, licensed under CC BY-NC 4.0

Keywords