Skip to main content

Quadratic functions

Graph of a quadratic function with the equation y equals x squared. The turning point occurs at x equals 0, y equals 0.

Quadratic functions have a distinct parabolic shape. Graphs of quadratic functions have applications in a wide range of fields, like modelling projectile motion, optimising business revenue, analysing population growth and designing bridges and arches. Use this resource to learn about parabolas and how to sketch them.

A quadratic function has the form:

\[y=ax^{2}+bx+c\] where \(a\neq0\).

The graph of a linear function is called a parabola.

Parabolas

To sketch a parabola, there are three components you must label.

  • The \(y\)-intercept is where the graph cuts the \(y\)-axis (\(x=0\)).
  • The \(x\)-intercepts are where the graph cuts the \(x\)-axis (\(y=0\)).
  • The turning point is the vertex of the parabola.

A parabola is a symmetrical about a vertical line that runs through the turning point.

Turning point

The \(a\) in the quadratic equation tells you some information about the shape of the parabola.

  • If \(a>0\), the parabola opens upwards and has a minimum turning point.
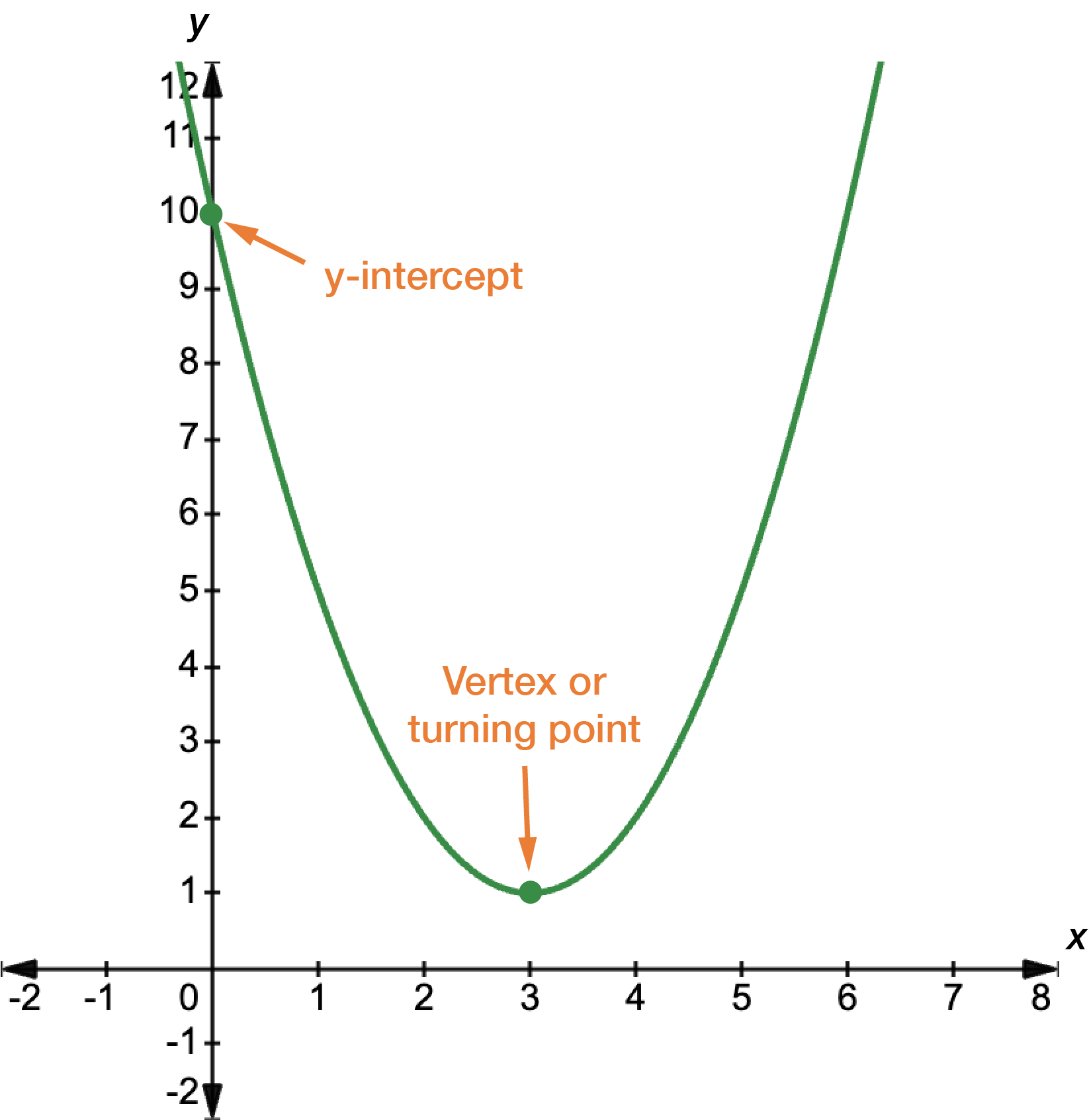
    Graph of a quadratic function. The parabola is labelled with its vertex or turning point and the y-intercept.
  • If \(a<0\), the parabola opens downwards and has a maximum turning point.
    Graph of a quadratic function. The inverted parabola is labelled with its vertex or turning point, y-intercept and two x-intercepts.

To find the \(x\)-coordinate of the turning point, you substitute \(b\) and \(a\) into the equation:

\[x=-\dfrac{b}{2a}\]

Then, you simply substitute the value of \(x\) into the quadratic equation to find the corresponding \(y\)-coordinate.

You can also write a quadratic function in turning point form:

\[y=a(x-h)^{2}+k\] where \((h,k)\) is the turning point.

Example 1 – finding the turning point

Find the turning point of \(y=(x-3)^{2}+4\).

The quadratic function has been written in turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 1(x-3)^{2}+4
\end{align*}\]

\(h=3\) and \(k=4\). The turning point is \((h,k)=(3,4)\).

Find the turning point of \(y=(x+5)^{2}+2\).

The quadratic function has been written in turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 1(x+5)^{2}+2
\end{align*}\]

\(h=-5\) and \(k=2\). The turning point is \((h,k)=(-5,2)\).

Find the turning point of \(y=2(x+1)^{2}\).

The quadratic function has been written in turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 2(x+1)^{2}+0
\end{align*}\]

\(h=-1\) and \(k=0\). The turning point is \((h,k)=(-1,0)\).

Find the turning point of \(y=x^{2}-7\).

We can rewrite the function in turning point form: \(y=(x-0)^{2}-7\).
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 1(x-0)^{2}-7
\end{align*}\]

\(h=0\) and \(k=-7\). The turning point is \((h,k)=(0,-7)\).

Alternatively, we can use the formula \(x=-\dfrac{b}{2a}\). In \(y=x^{2}-7\), \(a=1\) and \(b=0\). This gives us:
\[\begin{align*} x & = -\frac{0}{2(1)}\\
& = 0
\end{align*}\]

We substitute \(x=0\) into the equation to find the corresponding \(y\)-coordinate.
\[\begin{align*} y & = x^{2}-7\\
& = (0)^{2}-7\\
& = -7
\end{align*}\]

Therefore, the coordinates of the turning point are \((0,-7)\).

Find the turning point of \(y=6-(x-2)^{2}\).

We can rewrite the function in turning point form: \(y=-(x-2)^{2}+6\).
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = -1(x-2)^{2}+6
\end{align*}\]

\(h=2\) and \(k=6\). The turning point is \((h,k)=(2,6)\).

Exercise – finding the turning point

Find the turning point of the graphs of the following functions.

  1. \(y=(x-1)^{2}+5\)
  2. \(y=5(x-4)^{2}-12\)
  3. \(y=(x+2)^{2}+3\)
  4. \(y=-3(x+5)^{2}-3\)
  5. \(y=(x-6)^{2}\)
  6. \(y=-4x^{2}+3\)

  1. \((1,5)\)
  2. \((4,-12)\)
  3. \((-2,3)\)
  4. \((-5,-3)\)
  5. \((6,0)\)
  6. \((0,3)\)

Example 1 – graphing quadratic functions

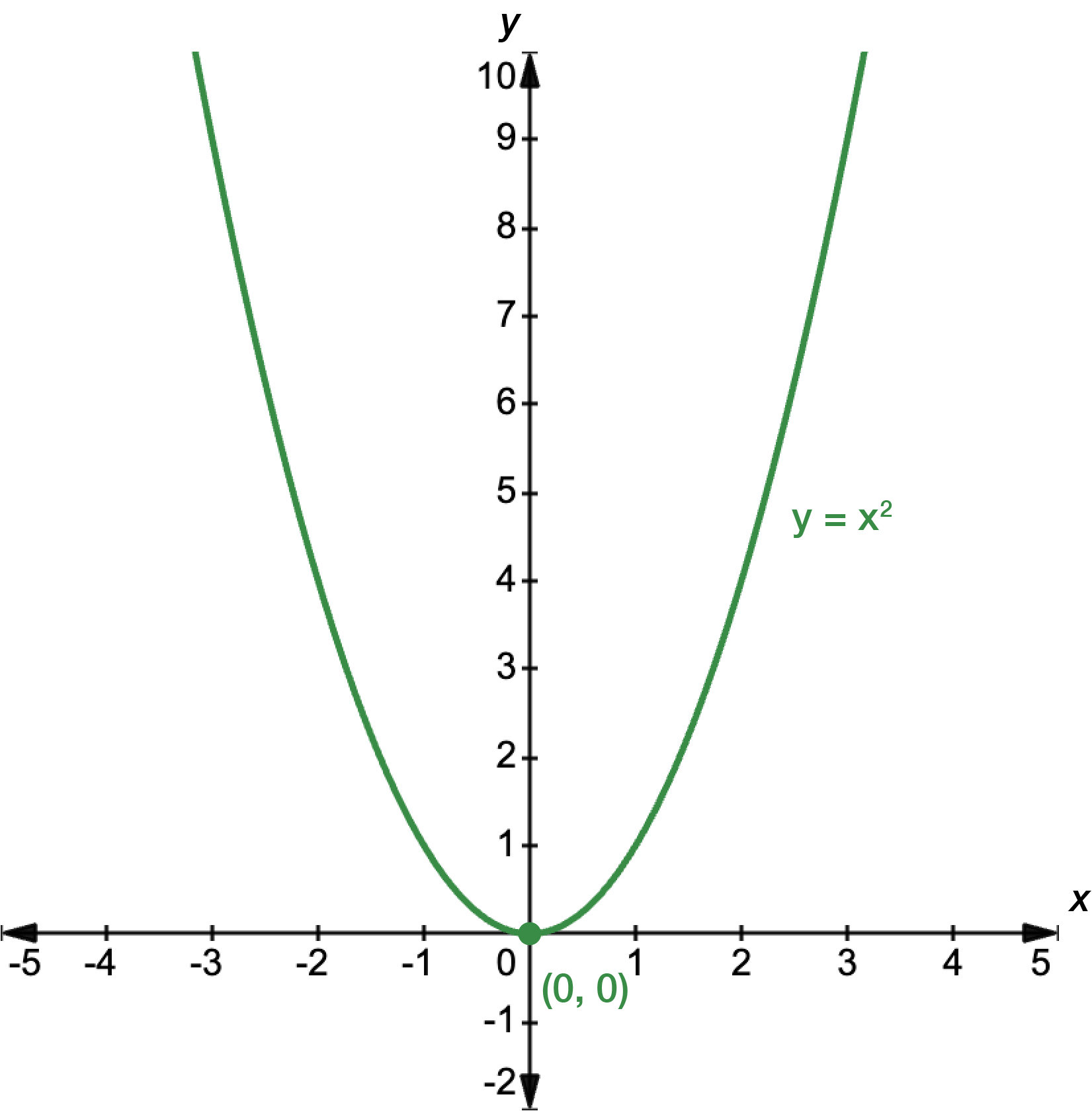
Sketch \(y=x^{2}\).

First, find the \(x\)- and \(y\)-intercepts. For \(x\), let \(y=0\).
\[\begin{align*} y & = x^{2}\\
0 & = x^{2}\\
x & = 0
\end{align*}\]

For \(y\), let \(x=0\).
\[\begin{align*} y & = x^{2}\\
& = 0^{0}\\
& = 0
\end{align*}\]

The graph intercepts the \(x\)-axis at \(x=0\), and the \(y\)-axis at \(y=0\). Next, we find the turning point. We can do this by rewriting the function in its turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 1(x-0)^{2}+0
\end{align*}\] \(h=0\) and \(k=0\), so the turning point occurs at \((0,0)\).

Sketch the graph, making sure to label the \(x\)- and \(y\)-intercepts, and the turning point.

Graph of a quadratic function with the equation y equals x squared. The turning point occurs at x equals 0, y equals 0.

Sketch \(y=(x-1)^{2}-2\).

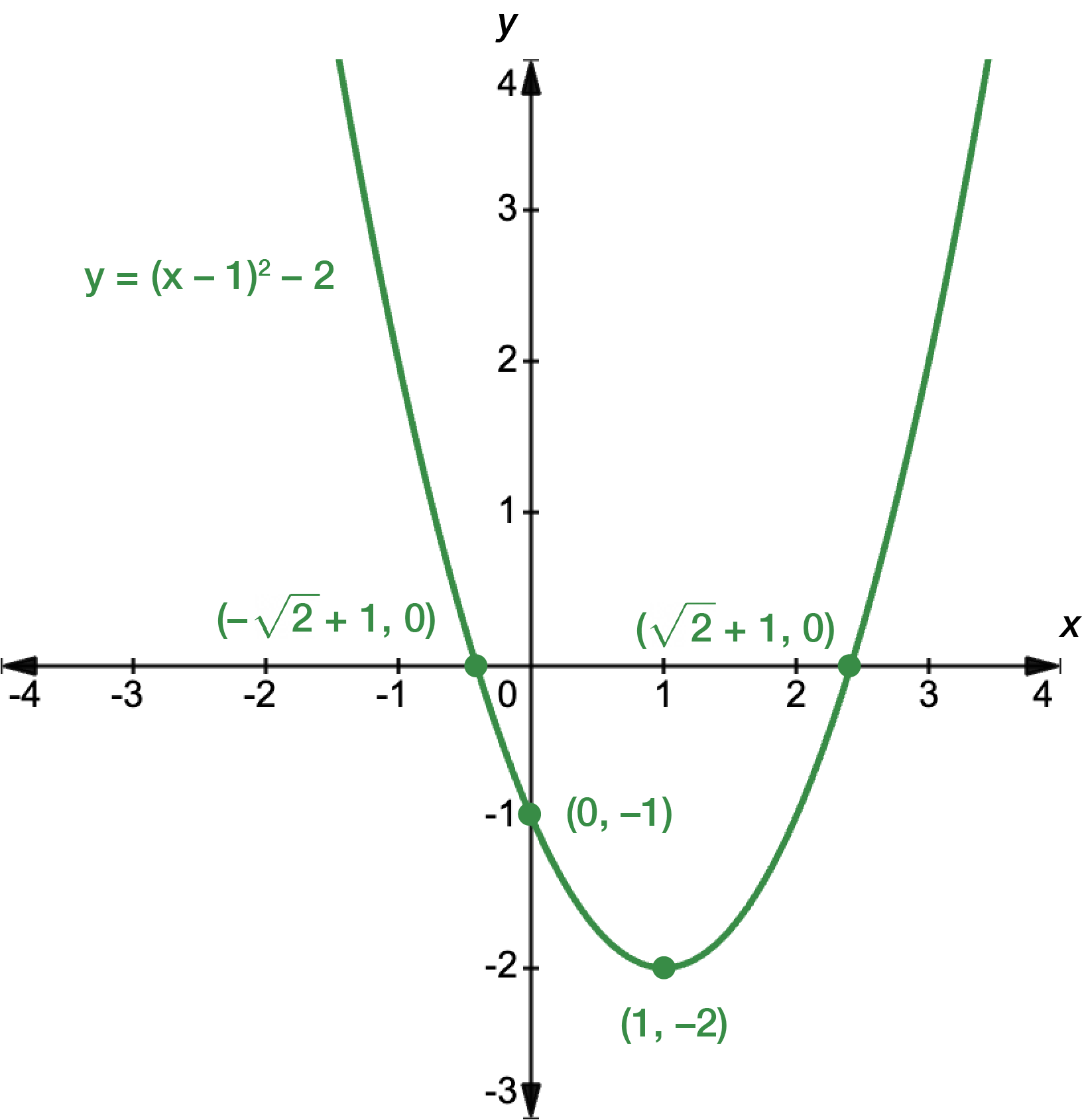
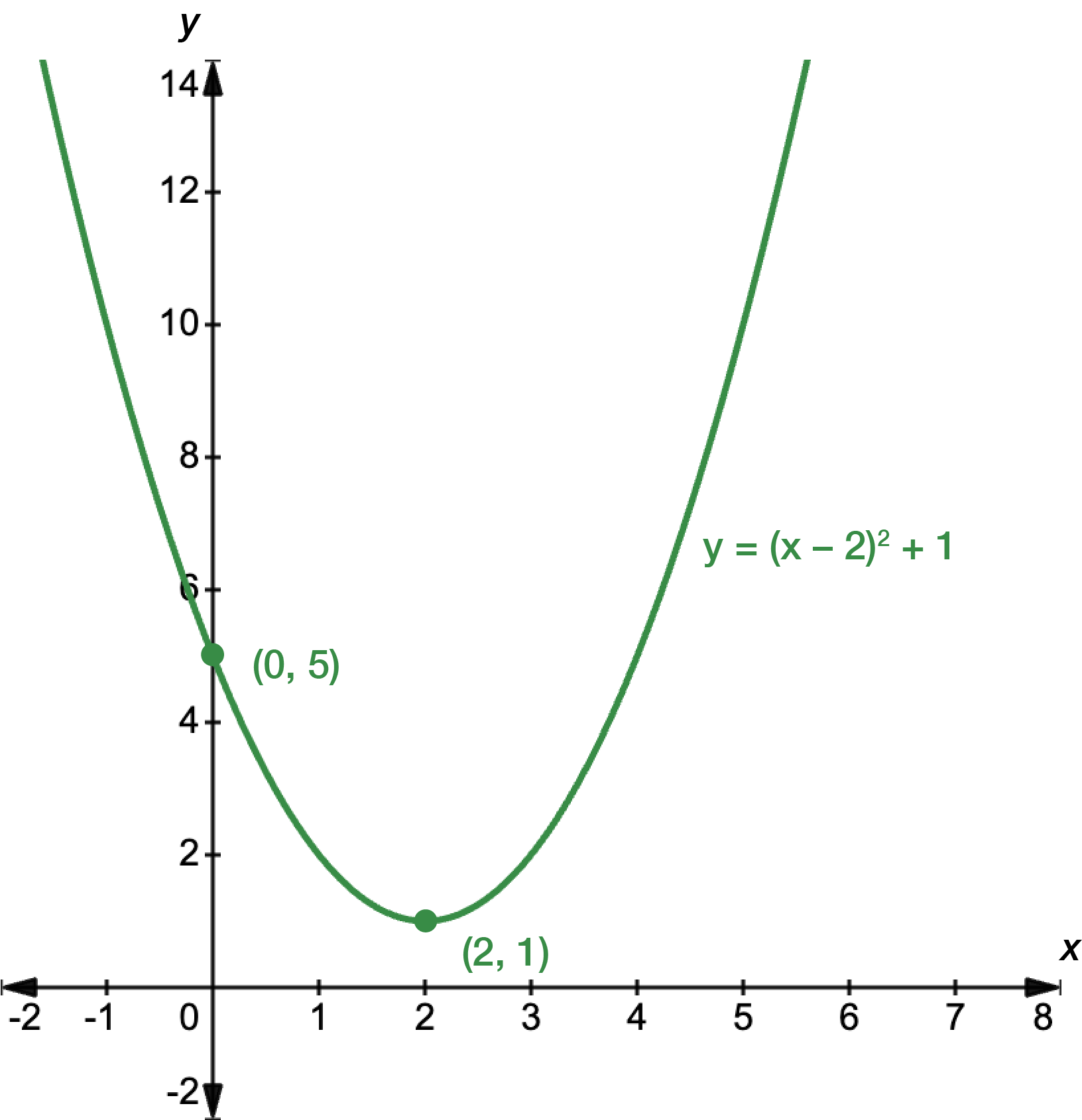
First, find the \(x\)- and \(y\)-intercepts. For \(x\), let \(y=0\).
\[\begin{align*} y & = (x-1)^{2}-2\\
0 & = (x-1)^{2}-2\\
2 & = (x-1)^{2}\\
\pm\sqrt{2} & = x-1\\
x & = \pm\sqrt{2}+1
\end{align*}\]

For \(y\), let \(x=0\).
\[\begin{align*} y & = (x-1)^{2}-2\\
& = (0-1)^{2}-2\\
& = 1-2\\
& = -1
\end{align*}\]

The graph intercepts the \(x\)-axis at \(x=-\sqrt{2}+1\) and \(x=\sqrt{2}+1\), and the \(y\)-axis at \(y=-1\). Next, we find the turning point. The function is already in turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 1(x-1)^{2}-2
\end{align*}\] \(h=1\) and \(k=-2\), so the turning point occurs at \((1,-2)\).

Sketch the graph, making sure to label the \(x\)- and \(y\)-intercepts, and the turning point.

Graph of a quadratic function with the equation y equals x minus 1 squared minus 2. The turning point occurs at x equals 1, y equals negative 2. The y-intercept is at negative 1. The x intercepts are at x equals negative square root 2 plus 1 and x equals square root 2 plus 1.

Sketch \(y=x^{2}+3\).

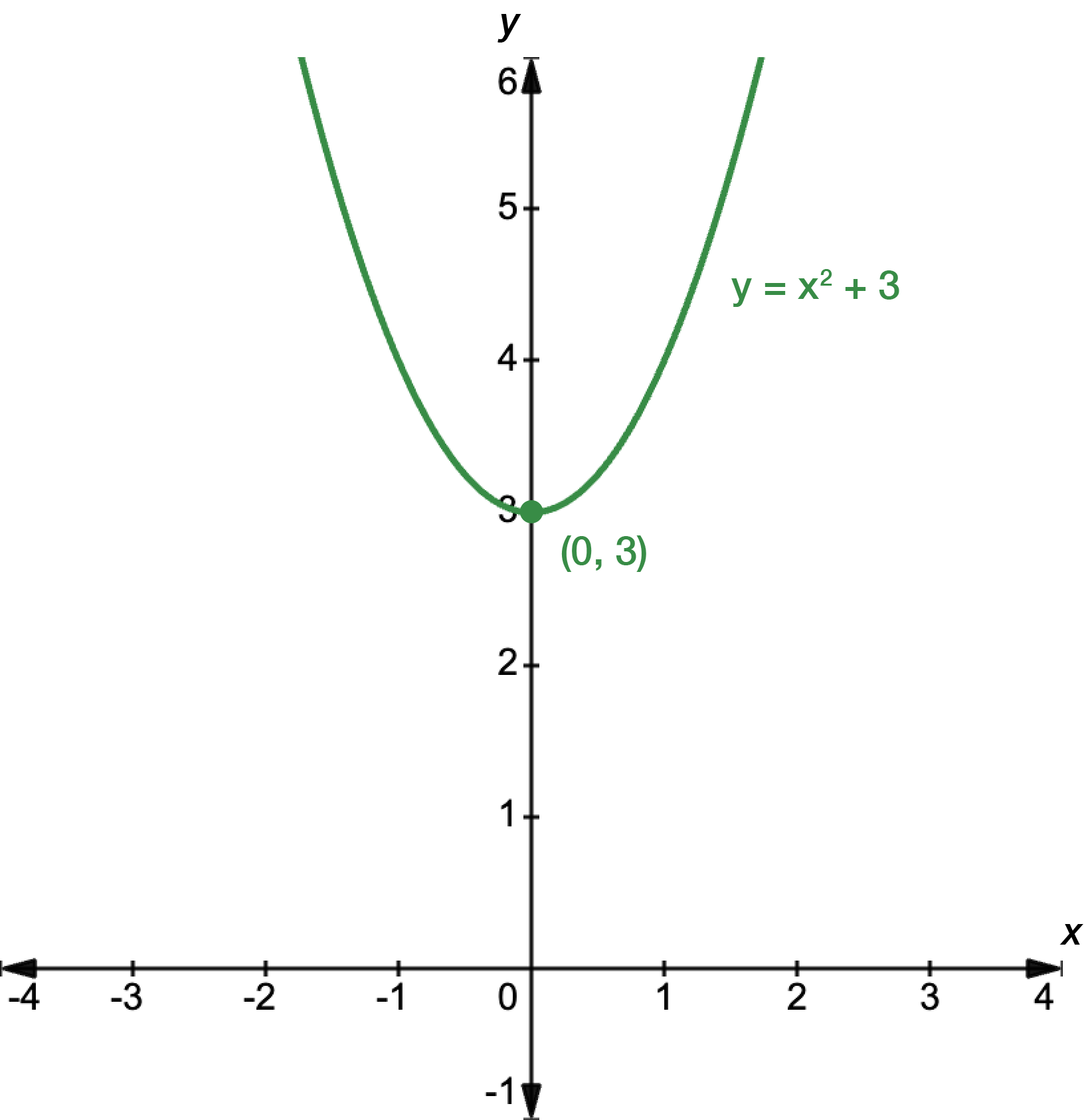
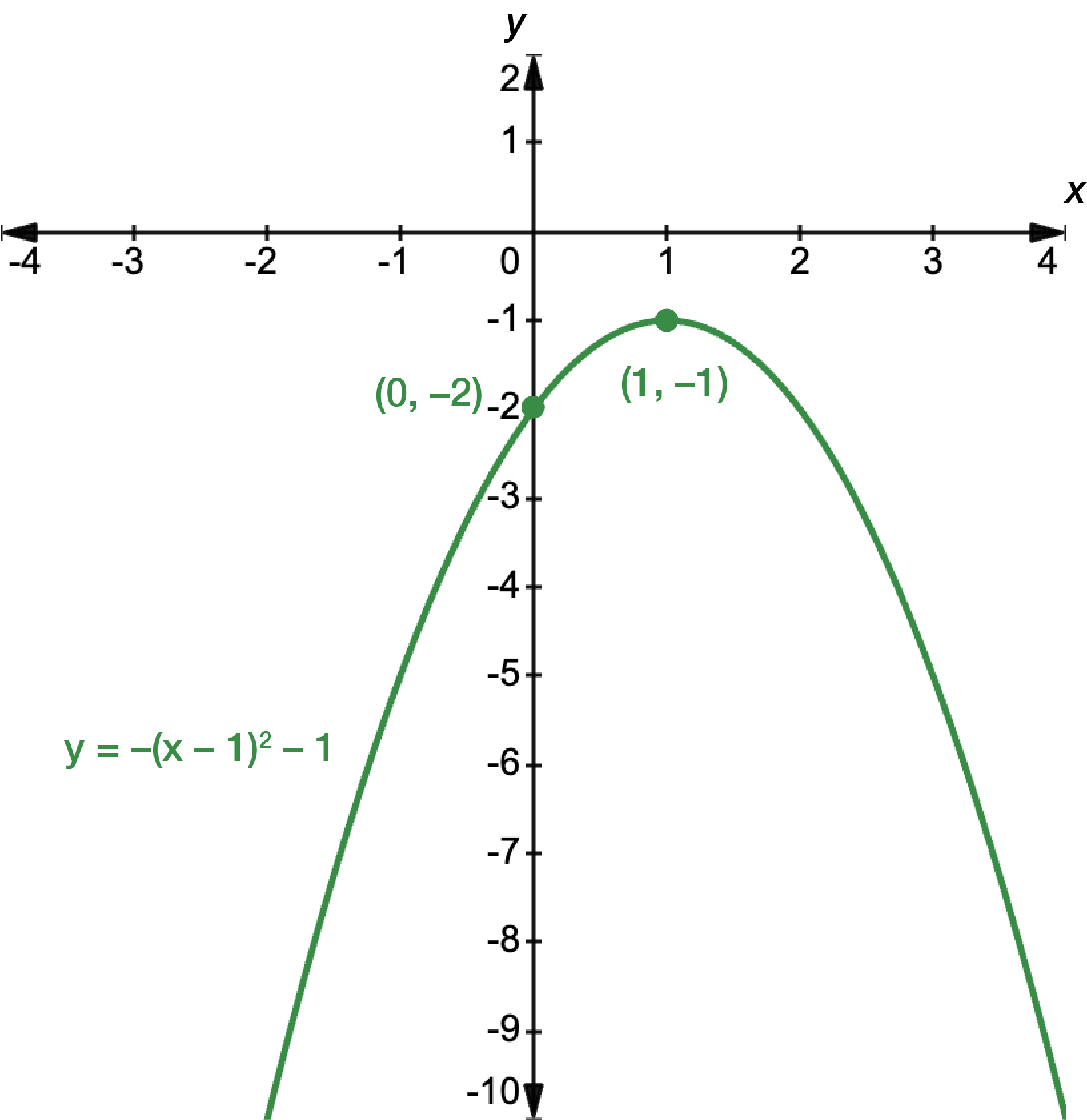
First, find the \(x\)- and \(y\)-intercepts. For \(x\), let \(y=0\).
\[\begin{align*} y & = x^{2}+3\\
0 & = x^{2}+3\\
-3 & = x^{2}\\
x & = \pm\sqrt{-3}
\end{align*}\]

\(\sqrt{-3}\) has no real solutions, so there are no \(x\)-intercepts, i.e. the graph does not touch the horizontal axis.

For \(y\), let \(x=0\).
\[\begin{align*} y & = x^{2}+3\
& = 0^{0}+3\\
& = 3
\end{align*}\]

The graph intercepts the \(y\)-axis at \(y=3\). Next, we find the turning point. We can do this by rewriting the function in its turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = 1(x-0)^{2}+3
\end{align*}\] \(h=0\) and \(k=3\), so the turning point occurs at \((0,3)\).

Sketch the graph, making sure to label the \(x\)- and \(y\)-intercepts, and the turning point.

Graph of a quadratic function with the equation y equals x squared plus 3. The turning point occurs at x equals 0, y equals 3.

Sketch \(y=4-2(x+3)^{2}\).

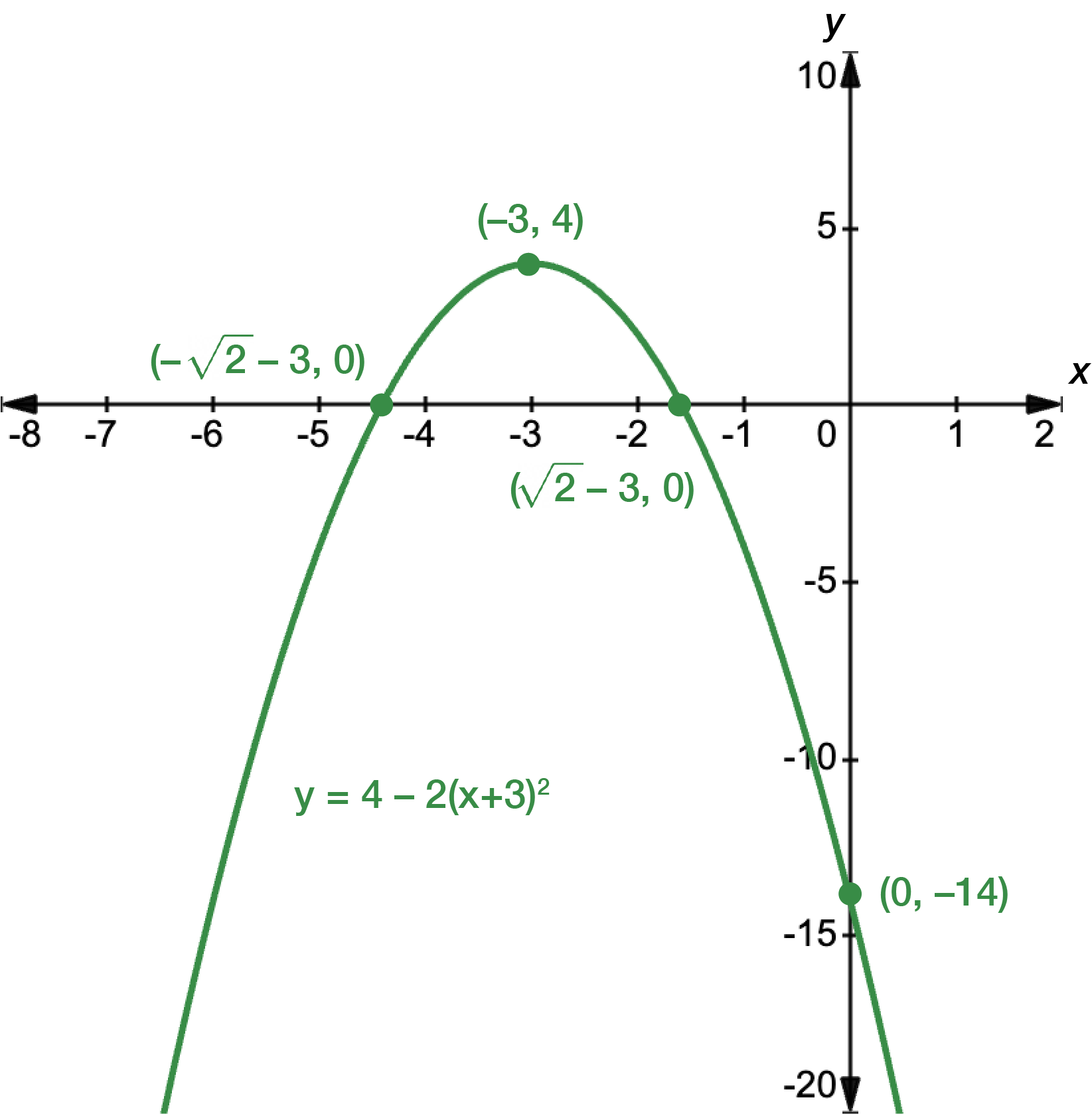
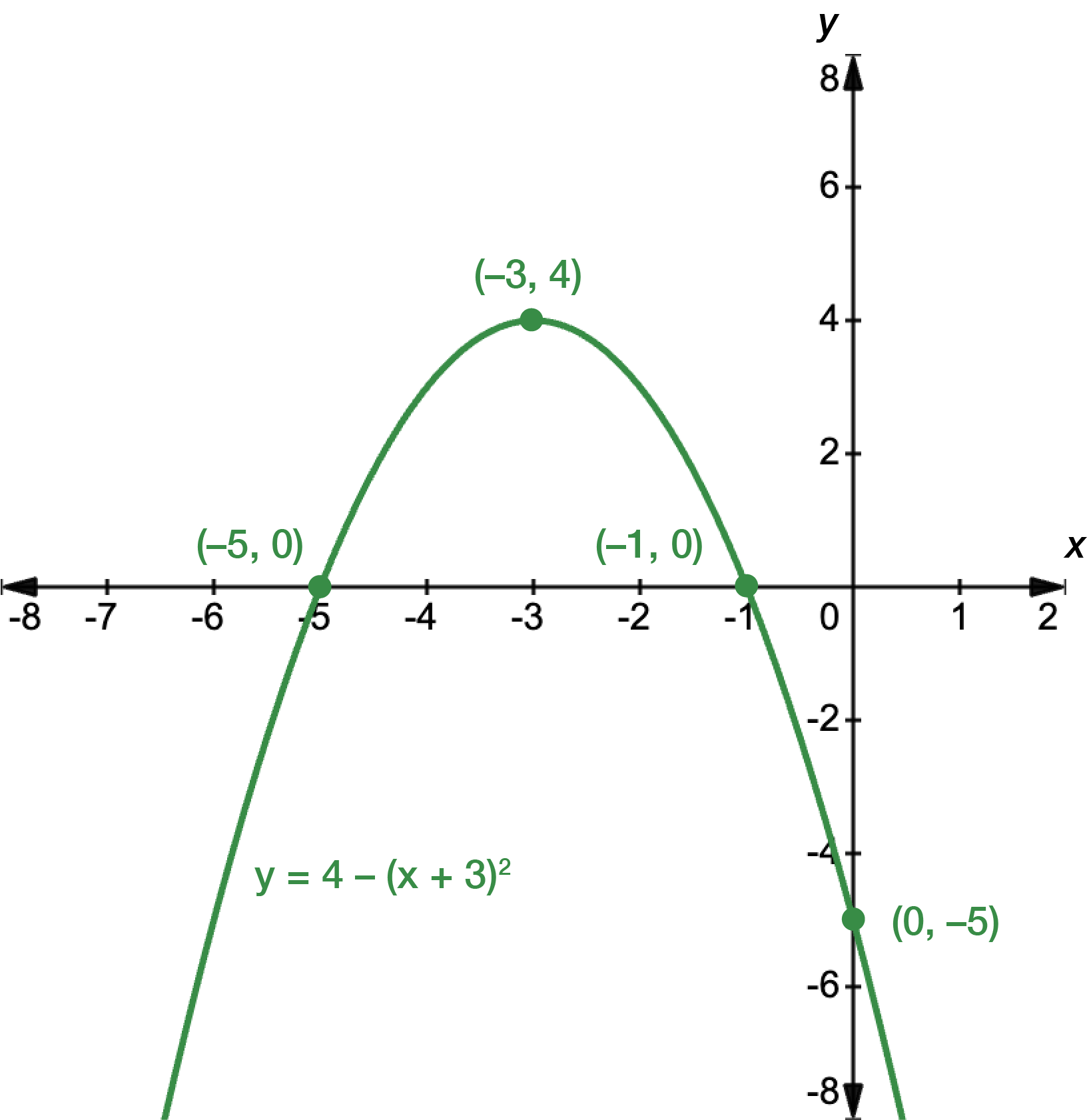
First, find the \(x\)- and \(y\)-intercepts. For \(x\), let \(y=0\).
\[\begin{align*} y & = 4-2(x+3)^{2}\\
0 & = 4-2(x+3)^{2}\\
4 & = 2(x+3)^{2}\\
2 & = (x+3)^{2}\\
\pm\sqrt{2} & = x+3\\
x & = \pm\sqrt{2}-3
\end{align*}\]

For \(y\), let \(x=0\).
\[\begin{align*} y & = 4-2(x+3)^{2}\\
& = 4-2(0+3)^{2}\\
& = 4-2(9)\\
& = 4-18\\
& = -14
\end{align*}\]

The graph intercepts the \(x\)-axis at \(x=-\sqrt{2}-3\) and \(x=\sqrt{2}-3\), and the \(y\)-axis at \(y=-14\). Next, we find the turning point. We can do this by rewriting the function in its turning point form.
\[\begin{align*} y & = a(x-h)^{2}+k\\
& = -2(x+3)^{2}+4
\end{align*}\]

\(h=-3\) and \(k=4\), so the turning point occurs at \((-3,4)\).

Sketch the graph, making sure to label the \(x\)- and \(y\)-intercepts, and the turning point.

Graph of a quadratic function with the equation y equals 4 minus 2 times x plus 3 squared. The turning point occurs at x equals negative 3, y equals 4. The y-intercept is at negative 14. The x intercepts are at x equals negative square root 2 minus 3 and x equals square root 2 minus 3.

Sketch \(y=x^{2}+2x-8\).

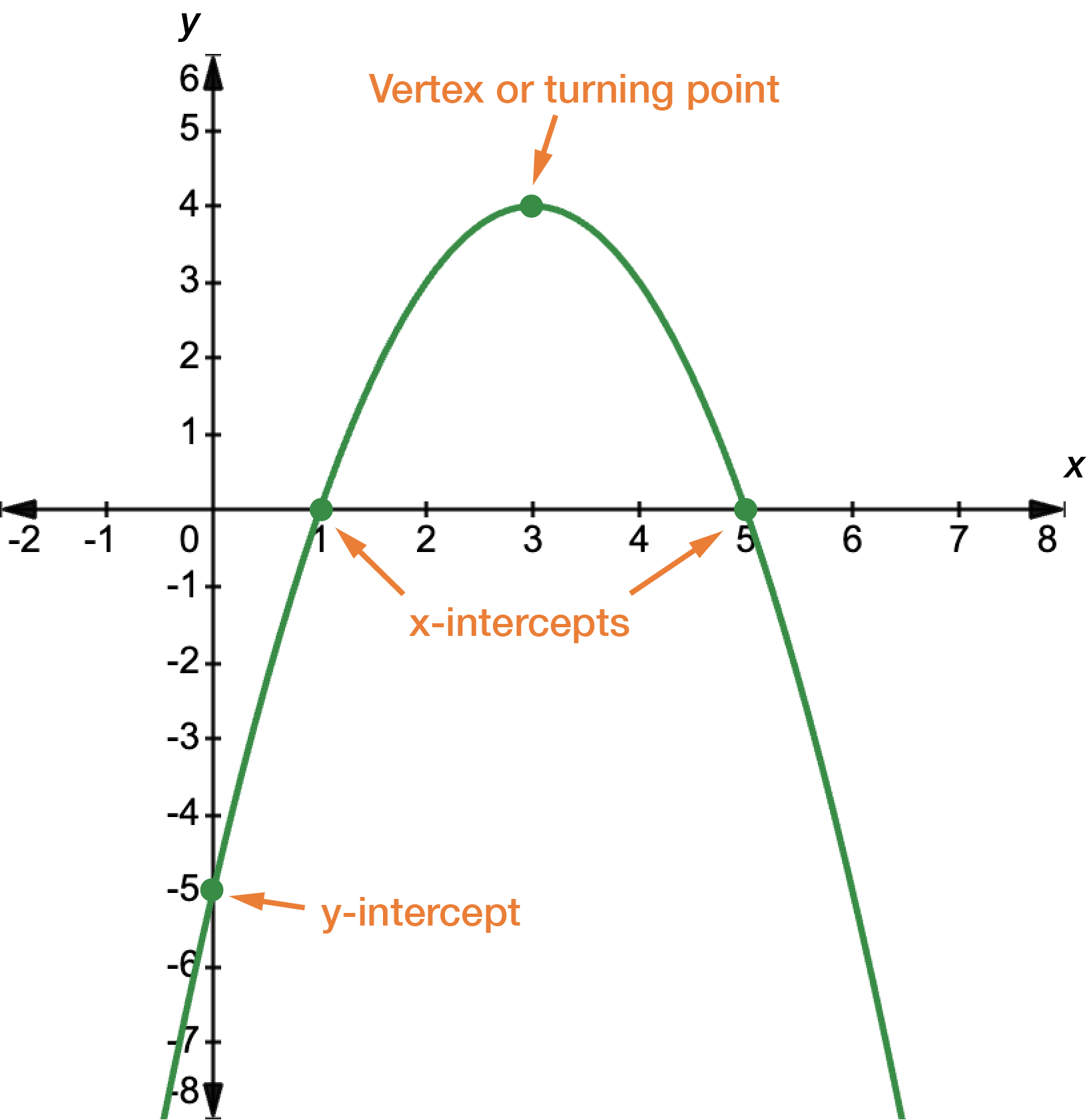
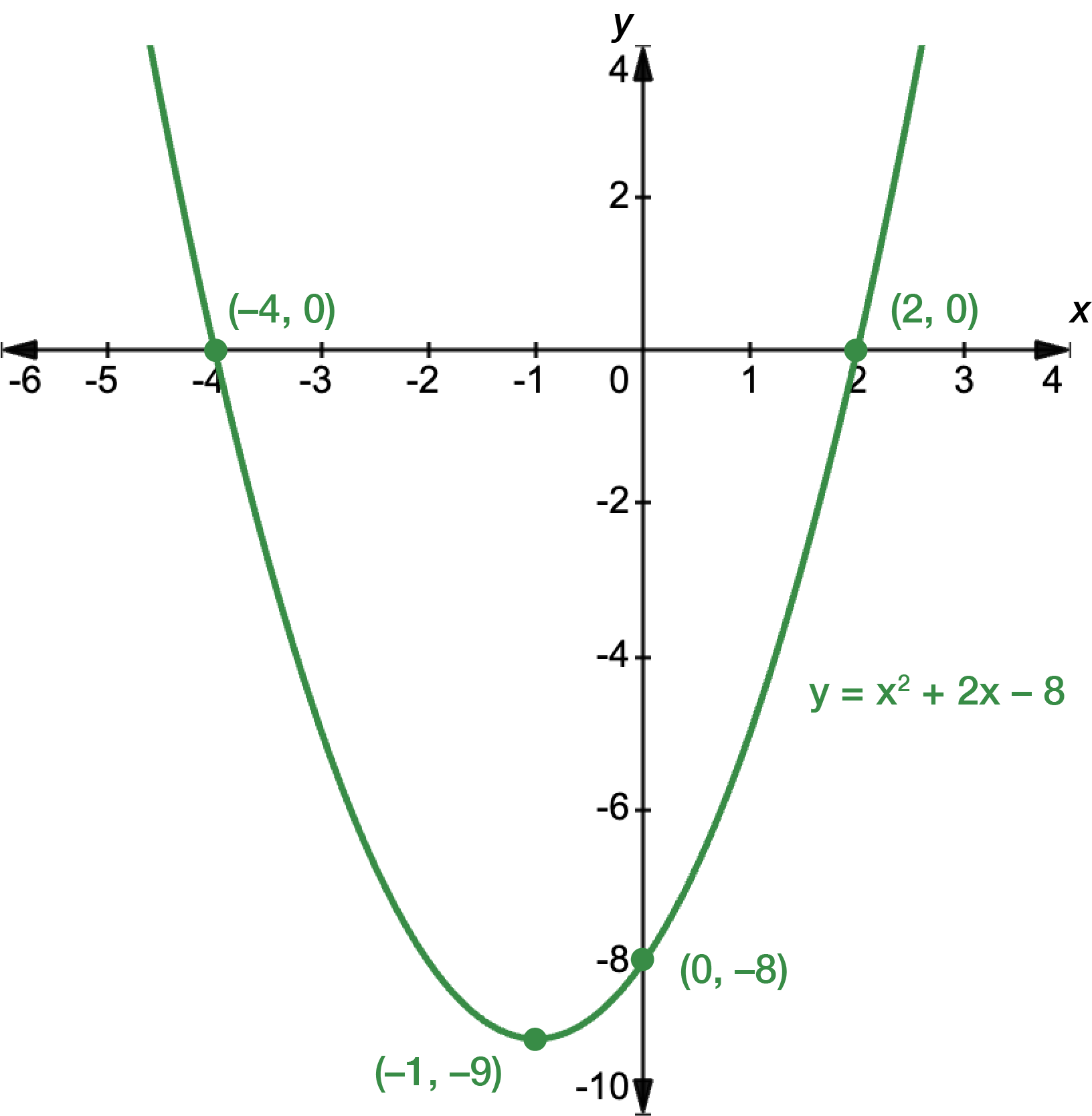
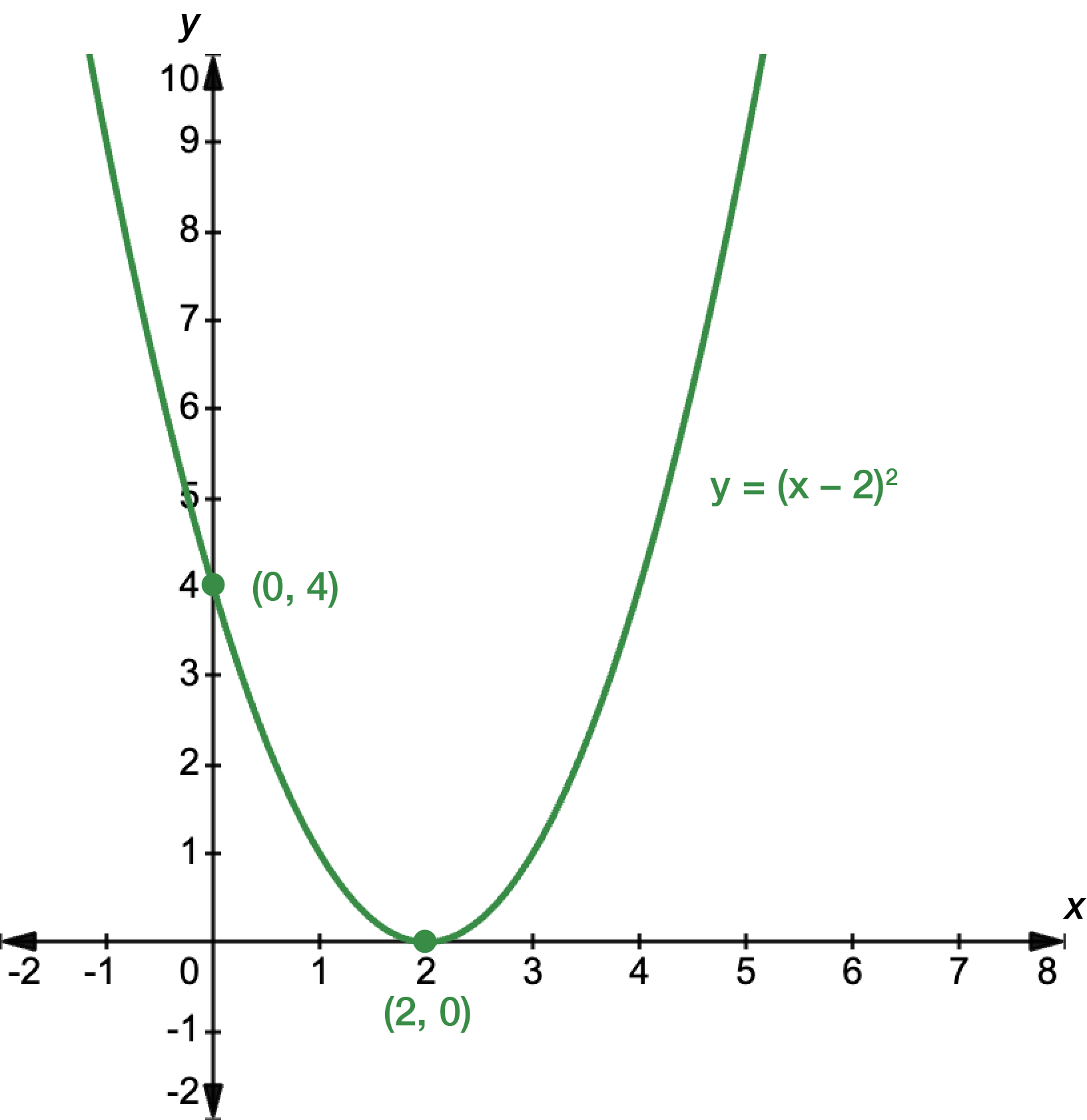
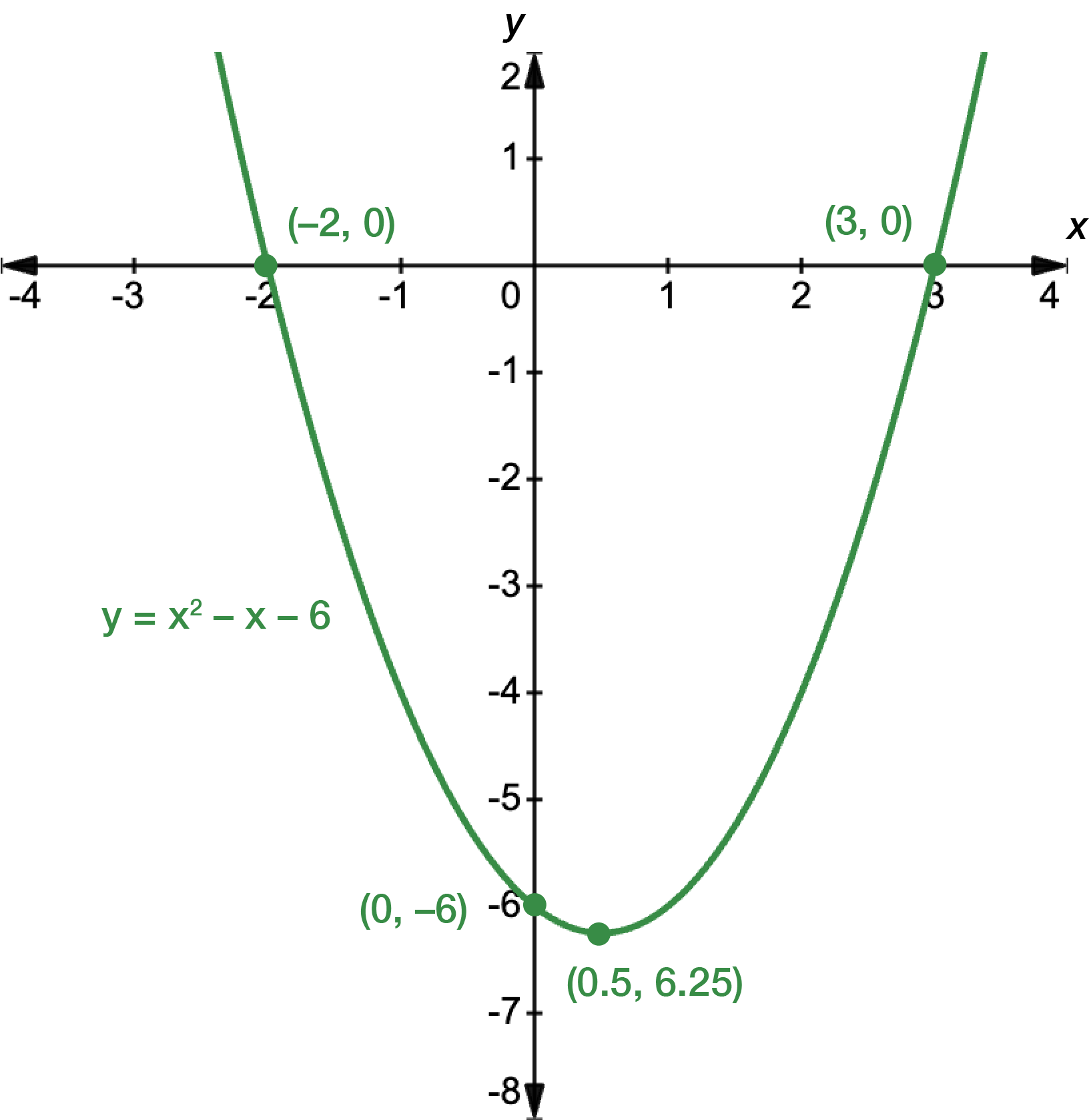
First, find the \(x\)- and \(y\)-intercepts. For \(x\), let \(y=0\).
\[\begin{align*} y & = x^{2}+2x-8\\
0 & = x^{2}+2x-8\\
0 & = (x+4)(x-2)\\
x+4=0 & \textrm{ or } x-2=0\\
x=-4 & \textrm{ or } x=2
\end{align*}\]

For \(y\), let \(x=0\).
\[\begin{align*} y = x^{2}+2x-8\\
& = (0)^{2}+2(0)-8\\
& = -8
\end{align*}\]

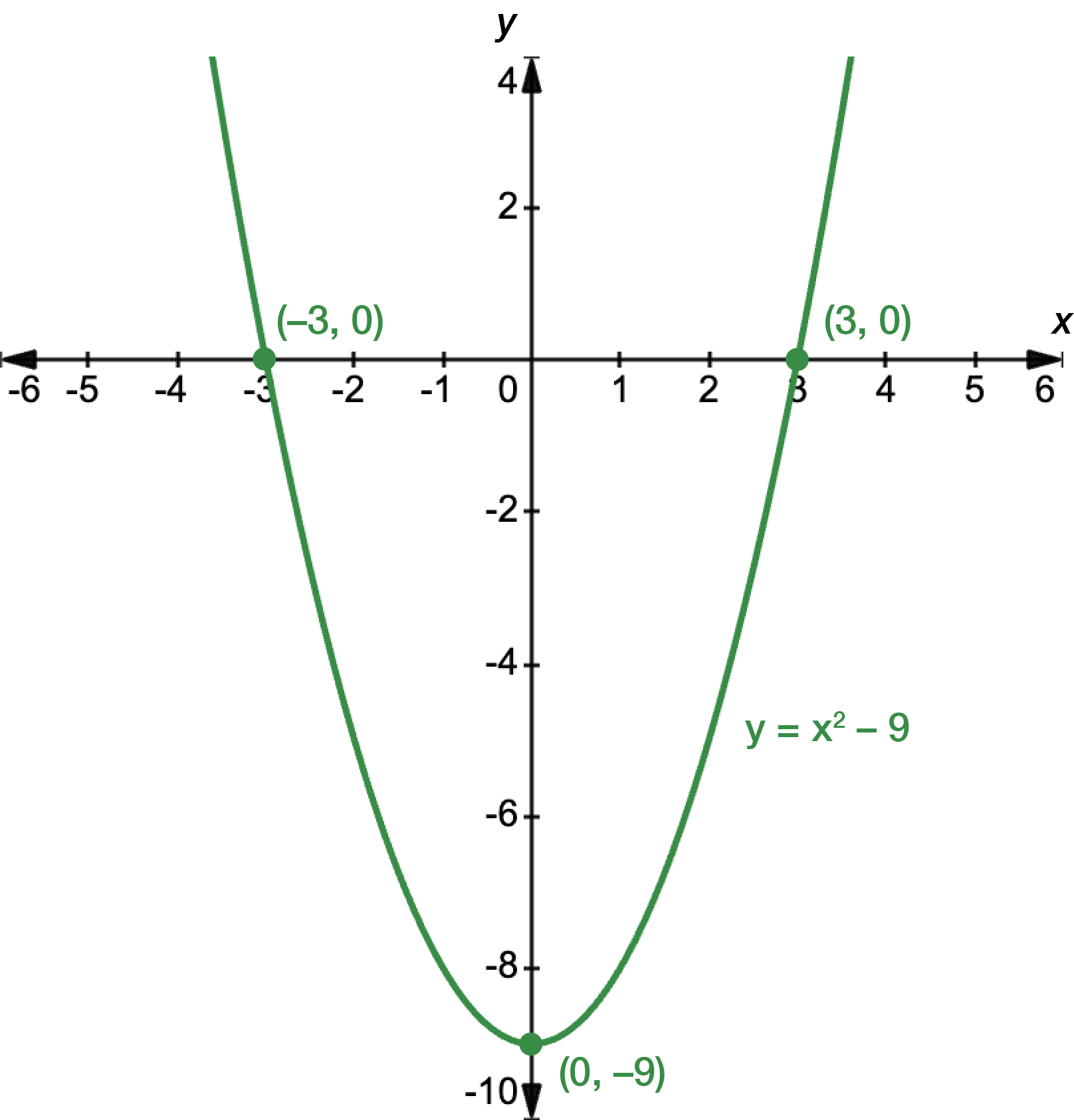
The graph intercepts the \(x\)-axis at \(x=-4\) and \(x=2\), and the \(y\)-axis at \(y=-8\). Next, we find the turning point. It is a bit challenging to rewrite the function in its turning point form, so we can just use \(x=-\dfrac{b}{2a}\).
\[\begin{align*} x & = -\frac{b}{2a}\\
& = -\frac{2}{2(1)}\\
& = -\frac{2}{2}\\
& = -1
\end{align*}\]

For the corresponding \(y\)-coordinate, we just substitute \(x=-1\) into the quadratic function.
\[\begin{align*} y & = x^{2}+2x-8\\
& = (-1)^{2}+2(-1)-8\\
& = 1-2-8\\
& = -9
\end{align*}\]

The turning point occurs at \((-1,-9)\).

Sketch the graph, making sure to label the \(x\)- and \(y\)-intercepts, and the turning point.

Graph of a quadratic function with the equation y equals x squared plus 2x minus 8. The turning point occurs at x equals negative 1, y equals negative 9. The y-intercept is at negative 8. The x intercepts are at x equals negative 4 and x equals 2.

Exercise – graphing quadratic functions

  1. Sketch graphs of the following.
    1. \(y=x^{2}-7\)
    2. \(y=(x-2)^{2}+1\)
    3. \(y=4-(x+3)^{2}\)
    4. \(y=(x-2)^{2}\)
    5. \(y=-(x-1)^{2}-1\)
  2. Sketch graphs of the following.
    1. \(y=x^{2}-x-6\)
    2. \(y=-x^{2}-2x+8\)
    3. \(y=x^{2}-4x\)
    4. \(y=-2x^{2}-6x\)
    5. \(y=x^{2}-9\)

    1. \(y=x^{2}-7\)
      Graph of a quadratic function with the equation y equals x squared minus 7. The turning point occurs at x equals 0, y equals negative 7. The y-intercept is at negative 7. The x intercepts are at x equals negative square root 7 and x equals square root 7.
    2. \(y=(x-2)^{2}+1\)
      Graph of a quadratic function with the equation y equals x minus 2 squared plus 1. The turning point occurs at x equals 2, y equals 1. The y-intercept is at 5.
    3. \(y=4-(x+3)^{2}\)
      Graph of a quadratic function with the equation y equals 4 minus x plus 3 squared. The turning point occurs at x equals negative 3, y equals 4. The y-intercept is at negative 5. The x intercepts are at x equals negative 5 and x equals negative 1.
    4. \(y=(x-2)^{2}\)
      Graph of a quadratic function with the equation y equals x minus 2 squared. The turning point occurs at x equals 2, y equals 0. The y-intercept is at 4.
    5. \(y=-(x-1)^{2}-1\)
      Graph of a quadratic function with the equation y equals negative x minus 1 squared minus 1. The turning point occurs at x equals 1, y equals negative 1. The y-intercept is at negative 2.
    1. \(y=x^{2}-x-6\)
      Graph of a quadratic function with the equation y equals x squared minus x minus 6. The turning point occurs at x equals 0.5, y equals 6.25. The y-intercept is at negative 6. The x intercepts are at x equals negative 2 and x equals 3.
    2. \(y=-x^{2}-2x+8\)
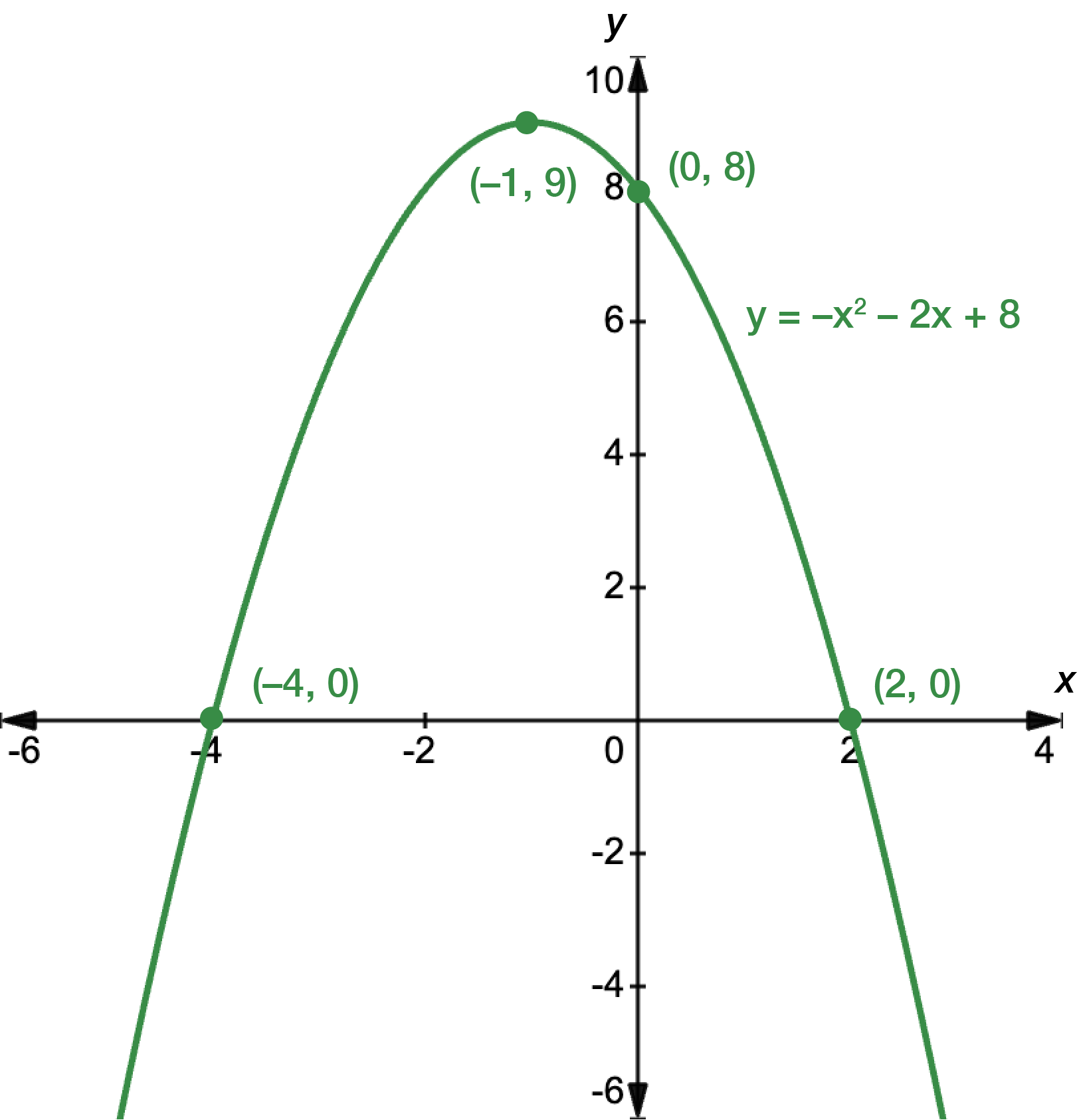
      Graph of a quadratic function with the equation y equals minus x squared minus 2x plus 8. The turning point occurs at x equals negative 1, y equals 9. The y-intercept is at 8. The x intercepts are at x equals negative 4 and x equals 2.
    3. \(y=x^{2}-4x\)
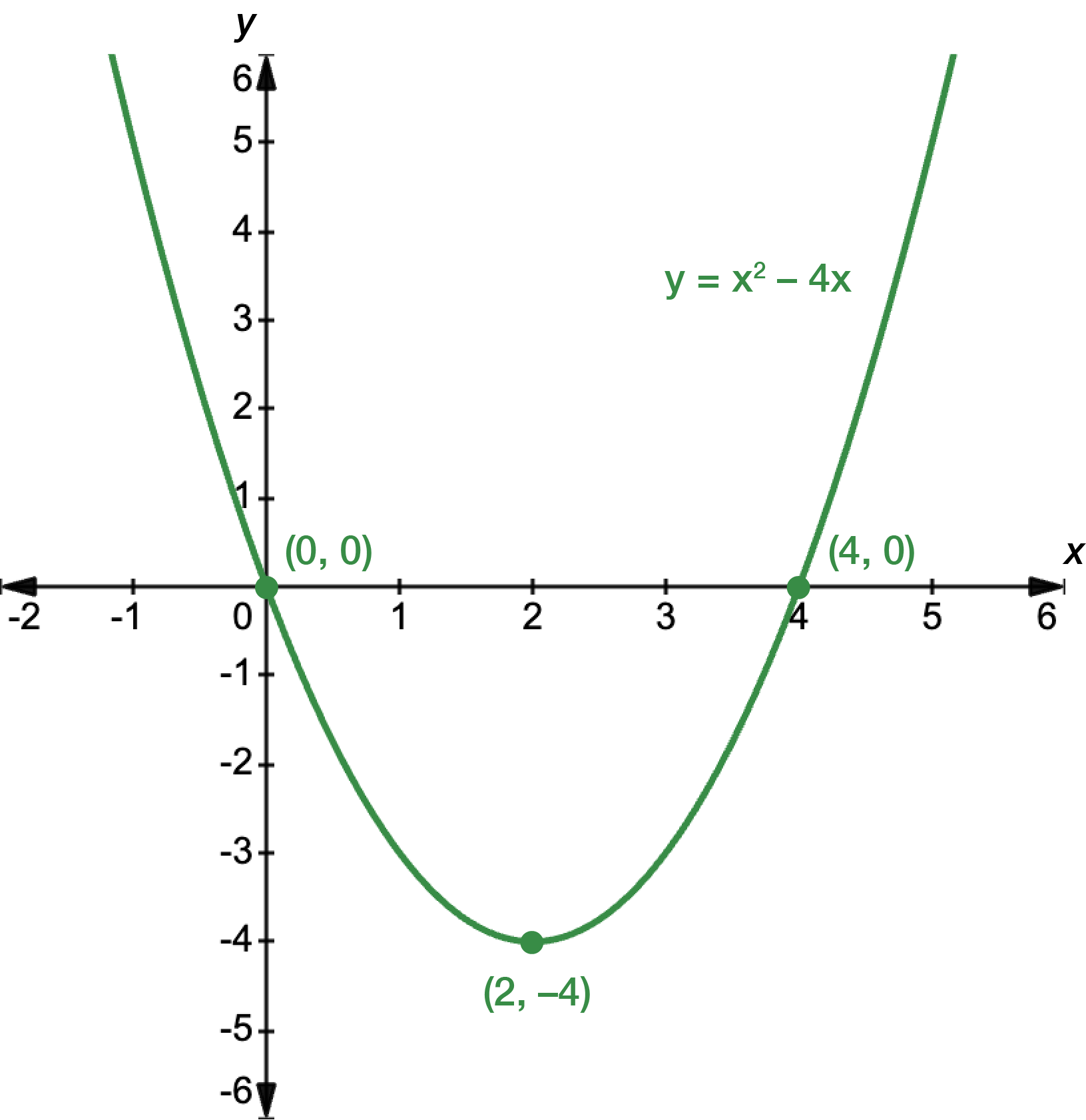
      Graph of a quadratic function with the equation y equals x squared minus 4x. The turning point occurs at x equals 2, y equals negative 4. The y-intercept is at 0. The x intercepts are at x equals 0 and x equals 4.
    4. \(y=-2x^{2}-6x\)
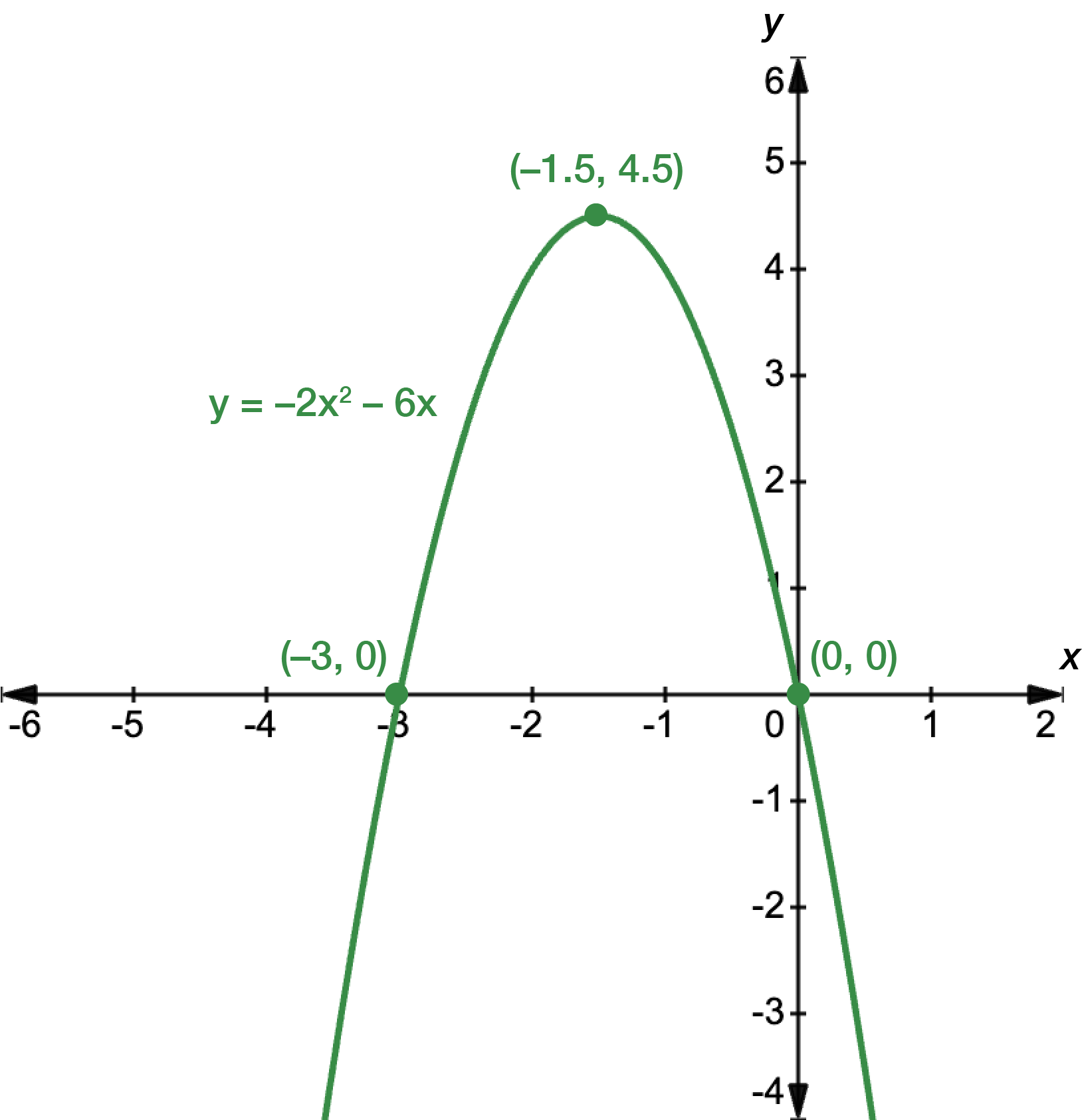
      Graph of a quadratic function with the equation y equals negative 2x squared minus 6x. The turning point occurs at x equals negative 1.5, y equals 4.5. The y-intercept is at 0. The x intercepts are at x equals negative 3 and x equals 0.
    5. \(y=x^{2}-9\)
      Graph of a quadratic function with the equation y equals x squared minus 9. The turning point occurs at x equals 0, y equals negative 9. The y-intercept is at negative 9. The x intercepts are at x equals negative 3 and x equals 3.

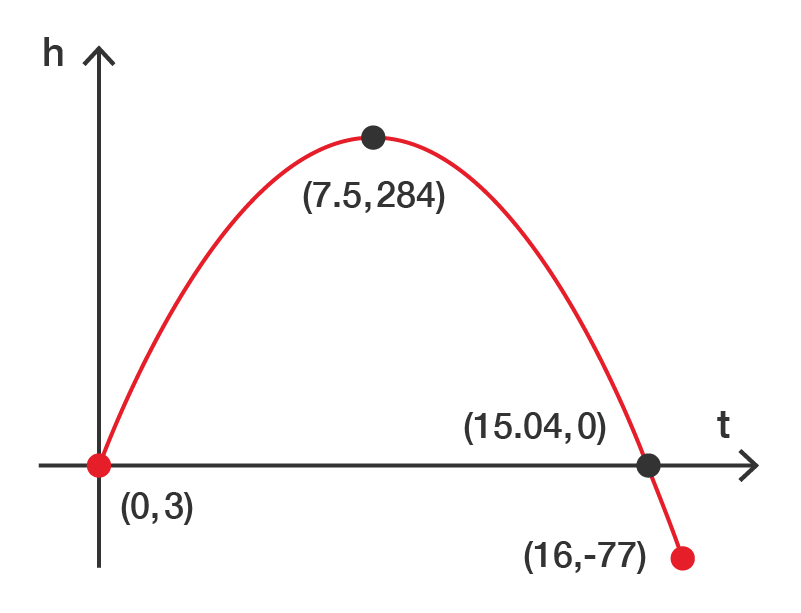
Images on this page by RMIT, licensed under CC BY-NC 4.0

Further resources

Factorisation

To find the \(x\)-intercepts for graphs of quadratic functions, you need to solve for \(x\). Sometimes, this involves factorising the quadratic, so make sure you are confident with this skill. Use this resource if you need a refresher!

Keywords