ILS2.1 Logarithms

Image: hmvierow, Pixabay
The modeling of growth and decay in areas such as finance, epidemiology and science makes use of equations with logarithms and exponentials. For example the equation \(\log_{e}\frac{N}{N_{0}}\approx-\lambda t\) is used to describe radioactive decay. The laws for working with logarithms enable us to solve equations that cannot be solved with other algebraic techniques.
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on logarithms.
A logarithm is an index but let’s look at an index first. Here’s the number eight, eight is the same as two to the power of three. Three things here, eight is the number, two is the base and three is the index, two to the power of three is two times two times two which is eight. So here it is again, eight equals two to the power of three. Now this can be written as log of eight to the base two equals three. Notice the three in red, the index three and the logarithm three. Also note the base two, both two to the three and log of eight to the base two. In other words we can write the equivalence here, A to the power of X is equal to N is the same as log of N to the base A is X. Notice the index in red and the logarithm in red.
Now look at some examples, five to the power of three is 125 which is the same as log of 125 to the base five is three. Notice in each case as I go through these that the index and the logarithm are shown in red. Here’s another one, three to the negative two is equal to one over nine, log of one over nine to the base three is negative two and finally 25 to the power of one half is five is the same as log of five to the base 25 is equal to the half. Study these carefully before moving on to the next slide.
Now let’s work out log of 64 to the base four. We’ll write the equivalent statement first and beneath that log of 64 to the base four which equals X is the same as four to the power of X is 64. In other words what we’re trying to do here is working out what the X value is, the power of four. So four cubed gives us 64, four times four times four, in other words X is equal to three, therefore log of 64 to the base four is equal to three.
Here’s another problem but this time we’re solving log of X to the base two equals five. In the previous slide we were working out what the logarithm was, here we’re working out what the number is, which is X in this case. First of all let’s write the equivalent statement and then plugging our log over X to the base two equals five into that equivalent statement gives us two to the power of five is equal to X. In other words we’re working out what two to the power of five is, which is two times two times two times two times two, which is 32, in other words X is equal to 32.
Now here are two important logarithm rules. The first rule is A to the power of zero is equal to one, which the same as log of one to the base A is equal to zero. In other words for any base the log of one is zero. Second rule is A to the power of one is equal to A or the log of A to the same base A is equal to one, in other words the log of any number with itself as base is equal to one.
There are three laws of logarithms that you must know. Here’s the first one. The log of two numbers multiplied together, M N is equal to the log of M plus the log of N. For instance here’s the log of 15 and 15 is five times three, so the log of five times three is equal to the log of five plus the log of three.
Here’s the second law. The log of a quotient, in other words M divided by N is equal to log of M minus log of N. So for instance if we have the log of 12 over five that is the same as log of 12 subtract the log of five and finally the log of a number to a power, in this case log of M to the power of P is the same as P log of M. Notice how the index here is now placed in front of the log. So for instance the log of nine to the power of two is the same as two log of nine but notice nine is the same as three squared so we can go one step further and write two log three squared, again using the law three squared we can place the two in front so it now becomes two times two log of three which is four log of three.
Now try some questions for yourselves. The answers to these problems are on the next slide. Thanks for watching this short movie.
Definition
The logarithm of a number is the power to which the base must be raised to produce the number. This means that a logarithm (or log) is an index. Every index or log expression contains a number, a base and an index. For example:
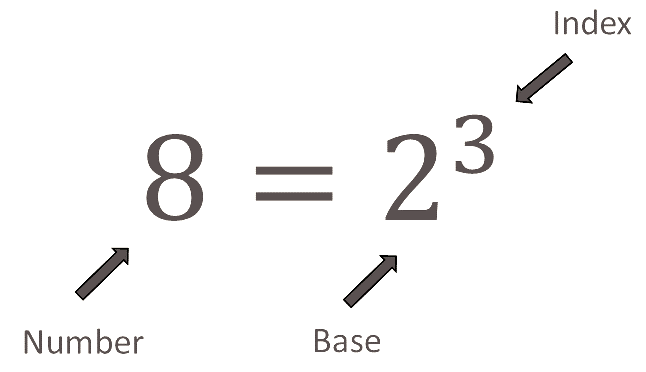
And we say " eight is equal to two to the power of three".
This statement has an equivalent logarithmic form and may be written as:
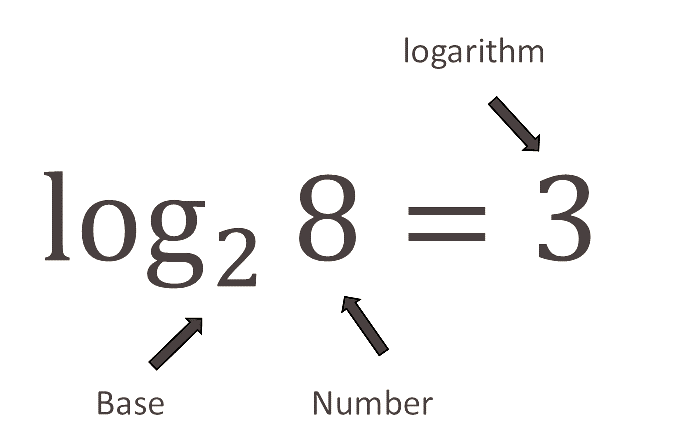
We say “the log to base two of eight is equal to three” (the power of two that gives eight is three).
Generally, providing \(a>0,\ n>0\) and \(a\neq1\),
\[ a^{x}=n\Leftrightarrow\log_{a}n=x \]
Logarithms and the Calculator
While any positive number except one can be the base of a logarithm, \(10\) and \(e\) are most common.
To find the power of \(10\) that produces \(50\) we use the LOG button on the calculator: \(\log_{10}50\approx1.7\) and \(10^{1.7}\approx50\).
To find the power of \(e\) that produces \(50\) we use the LN button on the calculator: \(\log_{e}50=\ln50\approx3.9\) and \(e^{3.9}\approx50\).
Examples
\(5^{3}=125\) \(\Leftrightarrow\log_{5}125\) \(=3\)
\(3^{-2}=\frac{1}{9}\Leftrightarrow\log_{3}\frac{1}{9}=-2\)
\(25^{\frac{1}{2}}=5\Leftrightarrow\log_{25}5=\frac{1}{2}\)
Evaluating Logarithms
To evaluate a logarithm it may be helpful to create an equation and change to index form.
Evaluate \(\log_{5}125\)
\[\begin{align*} \textrm{Let}\log_{5}125 & =x\\ 5^{x} & =125\textrm{ (change to index form)}\\ 5^{x} & =5^{3}\,\textrm{(express 125 as a power of 5)}\\ x & =3\,\textrm{(equating indices)}. \end{align*}\]Evaluate \(\log_{10}0.0001\) \[\begin{align*} \textrm{Let}\log_{10}0.0001 & =x\\ 10^{x} & =0.0001\textrm{ (change to index form)}\\ 10^{x} & =10^{-4}\,\textrm{(express 0.0001 as a power of 10})\\ x & =-4\,\textrm{(equating indices)}. \end{align*}\]
Three Important Properties of Logarithms
- For \(a>0,\) \[\begin{align*} a=1\Leftrightarrow\log_{a}1=0. \end{align*}\] That is, for any \(a>0,\) the log of 1 is zero.
- For \(a>0\) \[\begin{align*} a & =a^{1}\Leftrightarrow\log_{a}a=1. \end{align*}\]
- If \(\log_{a}m=\log_{a}p\) then \(m=p\).
Logarithm Laws
Corresponding to the three index laws, there are three laws of logarithms to help in manipulating logarithms. If \(m,n>0\) and \(a>0,\ a\neq1\) then
First Logarithm Law \[\begin{align*} \log_{a}(mn) & =\log_{a}m+\log_{a}n \end{align*}\]
Second Logarithm Law \[\begin{align*} \log_{a}\frac{m}{n} & =\log_{a}m-\log_{a}n \end{align*}\]
Third Logarithm Law \[\begin{align*} \log_{a}m^{p} & =p\log_{a}m \end{align*}\]
The laws can be used to simplify and evaluate logarithmic expressions
Examples
\(\log_{a}15=\log_{a}(5\times3)=\log_{a}5+\log_{a}3\)
\(\log_{a}\frac{12}{5}=\log_{a}12-\log_{a}5\)
\(\log_{a}\left(9^{2}\right)=2\log_{a}9=2\log_{a}3^{2}=4\log_{a}3\)
\(\log_{10}6+\log_{10}2=\log_{10}(6\times2)=\log_{10}12\)
\(\log_{3}6a+\log_{3}b-\log_{3}2a=\log_{3}\left(\frac{6a\times b}{2a}\right)=\log_{3}3b\)
Simplify \(\frac{1}{2}\log_{10}36-\log_{10}15+2\log_{10}5\)
\[\begin{align*} \frac{1}{2}\log_{10}36-\log_{10}15+2\log_{10}5 & =\log_{10}36^{\frac{1}{2}}-\log_{10}15+\log_{10}5^{2}\\ & =\log_{10}6-\log_{10}15+\log_{10}25\\ & =\log_{10}\frac{6\times25}{15}\\ & =\log_{10}10\\ & =1 \end{align*}\]
Logarithmic Equations
The laws of logarithms can be used to solve equations involving logarithms or in which the variable is a power.
Examples
Solve for \(x\) if \(\log(2x+1)=\log_{10}3\)
\[\begin{align*} \log_{10}(2x+1)= & \log_{10}3\\ 2x+1 & =3\\ x & =1 \end{align*}\]Solve for \(x\) if \(2^{x-3}=10\)
\[\begin{align*} 2^{x-3} & =10\\ \log_{10}2^{x-3} & =\log_{10}10\ \textrm{(take logs of both sides)}\\ (x-3)\log_{10}2 & =\log_{10}10\\ (x-3)(0.301) & =1\ (\textrm{use a calculator to find}\log_{10}2)\\ x-3 & =\frac{1}{0.301}\\ x & =3+\frac{1}{0.301}\\ x & =6.32 \end{align*}\]
Exercise 1
Write in logarithm form
a) \(3^{2}=9\)
b) \(10^{4}=10000\)
c) \(10^{-2}=0.01\)
d) \(e^{a}=b\)
\[\begin{array}{llll} a)\,\log_{3}9=2 & b)\,\log_{10}10000=4 & c)\,\log_{10}0.01=-2 & d)\,\log_{e}b=a.\end{array}\]
Exercise 2
Evaluate without using a calculator
a) \(\log_{7}49\)
b) \(\log_{10}\sqrt{10}\)
c) \(\log_{5}1\)
d) \(\log_{10}100000\)
e) \(\log_{5}5\)
\[\begin{array}{lllll} a)\,2 & b)\,1/2 & c)\,0 & d)\,5 & e)\,1\end{array}\]
Exercise 3
Simplify
a) \(\log_{4}8+\) \(\log_{4}3\) \(-\log_{4}2\)
b) \(\frac{1}{2}\log_{10}25-\) \(\log_{10}4\)+2\(\log_{10}3\)
c) \(\log_{e}e^{2}+2\) \(\log_{e}3-\) \(\log_{e}18\)
d) \(\log_{a}4+2\) \(\log_{a}3\)–\(2\log_{a}6\)
e) \(\frac{1}{2}\log_{10}a^{2}+3\) \(\log_{10}b-\) \(\log_{10}3ab^{2}\)
\[\begin{array}{lllll} a)\,\log_{4}12 & b)\,\log_{10}\left(45/4\right) & c)\,2-\log_{e}2 & d)\,0 & e)\,\log_{10}b-\log_{10}3\end{array}\]
Exercise 4
Solve for \(x\)
a) \(\log_{10}x=\log_{10}4-\log_{10}2\)
b) \(\log_{2}2x-\) \(2\log_{2}3\) \(=\) \(\log_{2}6\)
c) \(10^{m+1}=7\)
\[\begin{array}{lll} a)\,x=2 & b)\,x=27 & c)\,m=-0.155\end{array}\]
Download this page, ILS 2.1 Logarithms (PDF 315 KB)
What's next... ILS2.2 Exponential equations
