Chemical equations and reactions
A chemical reaction is represented by a chemical equation that involves ions, atoms and molecular formulas.
Main components of a chemical equation:
- Reactants: The starting materials of the reaction. Reactants are written on the left side of the equation.
- Products: The materials obtained at the end of the reaction and written on the right side of the equation.
- An arrow is drawn between the reactants and products pointing towards the products to designate a chemical change.
- Conditions required for the reaction to occur, for instance, pressure and temperature, are written above the arrow.
- Physical state of the substances involved: This is written next to the chemical formulas using brackets and abbreviations, as shown next. Solid - (s), Liquid - (l), Gas - (g), Aqueous solution (a substance dissolved in water) - (aq)
- Coefficient: The numbers written before the chemical formulas to balance the chemical equation. 1
Let's take the photosynthesis reaction that occurs in plants as an example. Photosynthesis produces glucose and oxygen in the presence of a pigment known as chlorophyll using sunlight, carbon dioxide and water, as illustrated below.
Photosynthesis equation
Writing and balancing chemical equations
Write the balanced chemical equation for the reaction between nitrogen gas and hydrogen gas to produce ammonia gas.
Step 1: Write the reactants and products of the chemical equation using correct symbols and formulas.
-
Reactants are written on the left side and, products are written on the right side. Use the plus sign to separate each reactant or product from others. \[ \ce{N}_{2}+\ce{H}_{2}\ce{\qquad}\ce{NH}_{3} \]
-
Place an arrow pointing towards the products between reactants and products. \[ \ce{N}_{2}+\ce{H}_{2}\ce{\rightarrow}\ce{NH}_{3} \]
Step 2: Balance the chemical equation using suitable coefficients.
In a balanced chemical equation, an equal number of atoms of each element involved must be present on both sides (i.e: left and right sides of the equation).
-
Choose one atom to balance first. Generally, it helps to start with the compound that is composed of the greatest number of atoms. First, focus on the element of that compound which has the highest number of atoms. Thus, choose hydrogen from ammonia to start the balancing. Ammonia contains three hydrogen atoms, while hydrogen on the left side has two atoms. Therefore, to balance the number of hydrogen atoms, six hydrogen atoms will be required for each side as six is the lowest possible number that both two and three can divide evenly. So, place two in front of ammonia and three in front of molecular hydrogen to obtain six hydrogen atoms on both sides. \[\begin{align*} 2\ce{NH}_{3} & \qquad2\times3=6\\ 3\ce{H}_{2} & \qquad3\times2=6\\ \ce{N}_{2}+3\ce{H}_{2} & \rightarrow2\ce{NH}_{3} \end{align*}\]
-
Next, balance the rest of the atoms in the selected compound. In this example, the next atom will be nitrogen. The right side has two nitrogen atoms and the left side also has two nitrogen atoms. Therefore, nitrogen is already balanced.
-
Balance the remaining elements in the equation. As the selected equation only contains two types of atoms, there are no more atoms left to be balanced. Otherwise, balance the remaining atoms.
Step 3: Do a final check to ensure all types of atoms in the equation are balanced.
At this point, the equation is balanced for both atoms present. Two nitrogen on both sides and six hydrogens on both sides. \[ \ce{N}_{2}+3\ce{H}_{2}\rightarrow2\ce{NH}_{3} \]
The following table summarises the total number of atoms for each element involved on each side of the equation.
| Left side | Right side | |
|---|---|---|
| \(\ce{N}\) | \(2\) | \(2\) |
| \(\ce{H}\) | \(3\times2=6\) | \(2\times3=6\) |
Step 4: Check whether the coefficients are in their lowest possible whole numbers.
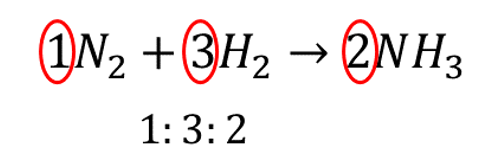
The ratio of \(1:3:2\) is the lowest possible in whole numbers.
Balance the following chemical equation
\(\ce{C}_{2}\ce{H}_{6}\ce{O}+\ce{O}_{2}\rightarrow\ce{CO}_{2}+\ce{H}_{2}\ce{O}\)
Step 1: Write the reactants and products of the chemical equation using correct symbols and formulas.
As the chemical equation is already given, this step is not applicable.
Step 2: Balance the chemical equation using suitable coefficients.
-
Choose one atom to balance first. Generally, it helps to start with the compound that is composed of the greatest number of atoms. Focus first on the element of that compound which has the highest number of atoms.
Therefore, start with hydrogen. The left side has six hydrogens, and the right side has two hydrogens. Placing three in front of water can give six hydrogen atoms on the right side as well. \[ \ce{C}_{2}\ce{H}_{6}\ce{O}+\ce{O}_{2}\rightarrow\ce{CO}_{2}+\ce{3H}_{2}\ce{O} \] -
Next, balance the carbon atoms. The left side contains two carbon atoms, and the right side contains one carbon atom. Using two as the coefficient for carbon dioxide makes two carbons on each side. \[ \ce{C}_{2}\ce{H}_{6}\ce{O}+\ce{O}_{2}\rightarrow\ce{2CO}_{2}+\ce{3H}_{2}\ce{O} \]
-
Finally, balance the oxygen atoms. The left side has three oxygen atoms, and the right side has seven oxygen atoms. Placing three in front of molecular oxygen on the left side gives seven oxygen atoms on each side. \[ \ce{C}_{2}\ce{H}_{6}\ce{O}+\ce{3O}_{2}\rightarrow\ce{2CO}_{2}+\ce{3H}_{2}\ce{O} \]
Step 3: Do a final check to ensure all types of atoms in the equation are balanced.
| Left side | Right side | |
|---|---|---|
| \(\ce{H}\) | \(6\) | \(3\times2=6\) |
| \(\ce{C}\) | \(2\) | \(2\) |
| \(\ce{O}\) | \(1+\left(3\times2\right)=7\) | \(\left(2\times2\right)+3=7\) |
Step 4: Check whether the coefficients are in their lowest possible whole numbers.

The ratio of \(1:3:2:3\) is the smallest possible whole number for the given equation.
Write and balance the chemical equation for the decomposition of hydrogen peroxide in the presence of light to water and oxygen gas.
Step 1: Write the reactants and products of the chemical equation using correct symbols and formulas.
Reactants: Hydrogen peroxide
Products: Water and oxygen gas
Write the reactants on the left side and products on the right side of the equation. Then place an arrow pointing towards the products. \[ \ce{H}_{2}\ce{O}_{2}\rightarrow\ce{H}_{2}\ce{O}+\ce{O}_{2} \]
Step 2: Balance the chemical equation using suitable coefficients. \[ \ce{H}_{2}\ce{O}_{2}\rightarrow\ce{H}_{2}\ce{O}+\ce{O}_{2} \]
| Left side | Right side | |
|---|---|---|
| \(\ce{H}\) | \(2\) | \(2\) |
| \(\ce{O}\) | \(2\) | \(3\) |
According to the above table, hydrogen is already balanced. There are two oxygen atoms on the left side and three oxygen atoms on the right side. The number of oxygen atoms can be balanced by placing \(\frac{1}{2}\) in front of molecular oxygen. This gives two oxygen atoms on each side: \[ \ce{H}_{2}\ce{O}_{2}\rightarrow\ce{H}_{2}\ce{O}+\frac{1}{2}\ce{O}_{2} \]
Step 3: Do a final check to ensure all types of atoms in the equation are balanced.
At this point, the equation is balanced for both atoms present. Two hydrogens on both sides and two oxygens on both sides.
| Left side | Right side | |
|---|---|---|
| \(\ce{H}\) | \(2\) | \(2\) |
| \(\ce{O}\) | \(2\) | \(2\) |
Step 4: Check whether the coefficients are in their lowest possible whole numbers.
\[ \ce{H}_{2}\ce{O}_{2}\rightarrow\ce{H}_{2}\ce{O}+\frac{1}{2}\ce{O}_{2} \] Except for the coefficient of oxygen on the right side of the equation, the rest have whole number coefficients. To make all coefficients in their smallest whole number, multiply all coefficients by two. \[ \ce{2H}_{2}\ce{O}_{2}\rightarrow\ce{2H}_{2}\ce{O}+\ce{O}_{2} \]
1 According to the law of conservation of mass, none of the atoms disappear during the reaction. However, atoms rearrange to form new chemicals. Therefore the total number of atoms of each type must be equal to that on the other side.
