Inverse of a 3×3 matrix

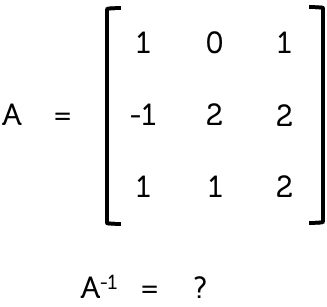
Being able to find the inverse of a \(3\times3\) matrix will help to simplify complex problems and enhances your ability to perform matrix operations efficiently. This is crucial in fields like engineering, physics and computer science.

Before you read further, make sure that you are familiar with augmented matrices and elementary row operations.

Inverting \(3\times3\) matrices

Unlike \(2\times2\) matrices, finding the inverse of \(3\times3\) matrices is a bit more complicated.

Let's consider matrix \(A\):

\[\left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array} \right] \]

There are a few methods to find the inverse of a \(3\times3\) matrix, but here, we will use the following method:

1. Rewrite the matrix in the form of an augmented matrix with matrix \(A\) as the coefficient matrix and the \(3\times3\) identity matrix as the constant matrix: \(\left[A|I\right]\).
   \[\left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\
   a_{21} & a_{22} & a_{23}\\
   a_{31} & a_{32} & a_{33}
   \end{array}
   \left|
   \begin{array}{ccc} 1 & 0 & 0 \\
   0 & 1 & 0\\
   0 & 0 & 1
   \end{array} \right. \right] \]
2. Use elementary row operations to reduce \(A\) to \(I\), or in other words, make \(A\) look like \(I\).
   \[\left[ \begin{array}{ccc} 1 & 0 & 0 \\
   0 & 1 & 0\\
   0 & 0 & 1
   \end{array}
   \left|
   \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\
   b_{21} & b_{22} & b_{23}\\
   b_{31} & b_{32} & b_{33}
   \end{array} \right. \right] \]Remember that because it is an augmented matrix, any operations applied to matrix \(A\) on the left-hand side must be applied to the identity matrix on the right-hand side.
3. Once \(A\) is transformed into the identity matrix, the final form on the right-hand side is the inverse of \(A\).
   \[A^{-1} = \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\
   b_{21} & b_{22} & b_{23}\\
   b_{31} & b_{32} & b_{33}
   \end{array} \right] \]

A square matrix ONLY has an inverse if its determinant is not equal to \(0\).

Elementary row operations

Rememeber the elementary row operations:

1. multiplication of a row by a constant
2. addition and subtraction of a multiple of a row to another row
3. interchanging two rows.

When using elementary row operations to find the inverse, there is a preferred order to achieve the identity matrix:

\[\begin{align*} \underbrace{ \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array} \right]}_{\textrm{Original matrix}} \rightarrow \underbrace{ \left[ \begin{array}{ccc} 1 & a_{12} & a_{13}\\
0 & a_{22} & a_{23}\\
0 & a_{32} & a_{33}
\end{array}\right]}_{a_{11}=1,\,a_{21}=a_{23}=0} \rightarrow \underbrace{ \left[ \begin{array}{ccc} 1 & a_{12} & a_{13}\\
0 & 1 & a_{23}\\
0 & a_{32} & a_{33}
\end{array} \right]}_{a_{22}=1}\\
\rightarrow \underbrace{ \left[ \begin{array}{ccc} 1 & 0 & a_{13}\\
0 & 1 & a_{23}\\
0 & 0 & a_{33}
\end{array} \right]}_{a_{12}=a_{32}=0} \rightarrow \underbrace{ \left[ \begin{array}{ccc} 1 & 0 & a_{13}\\
0 & 1 & a_{23}\\
0 & 0 & 1
\end{array} \right]}_{a_{31}=1} \rightarrow \underbrace{ \left[ \begin{array}{ccc} 1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{array} \right]}_{a_{13}=a_{23}=0}
\end{align*}\] If this looks confusing and a bit scary, don’t worry. It's easier to understand how this works with examples containing actual numbers.

Example 1 – finding the inverse of \(3\times3\) matrices

Find the inverse of the matrix \(A = \left[ \begin{array}{ccc} 1 & 0 & 1\\
-1 & 2 & 2\\
1 & 1 & 2
\end{array} \right]\).

First, set up the augmented matrix \(\left[A|I\right]\):

\[\left[ A|I \right] = \left[ \begin{array}{ccc} 1 & 0 & 1\\
-1 & 2 & 2\\
1 & 1 & 2
\end{array}
\left|
\begin{array}{ccc} 1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{array} \right. \right] \]

We now use elementary row operations to reduce the matrix on the left-hand side (LHS) to the identity matrix.

We already have a \(1\) in the \(a_{11}\) position of the LHS matrix, so we first make \(a_{21}=a_{31}=0\). We can show this by writing the original augmented matrix, followed by the equations in the middle for the row operations, then the new augmented matrix.

The next step is to make \(a_{22}=1\) in the LHS matrix. There are two ways to do this. We could divide \(R_{2}\) by \(2\); however, this introduces a fraction that may be awkward. Fractions are often required, but we will avoid using them until absolutely necessary.

The other way is to interchange \(R_{2}\) and \(R_{3}\).

\[\begin{align*} \left[ \begin{array}{ccc} 1 & 0 & 1\\
0 & 2 & 3\\
0 & 1 & 1
\end{array}
\left|
\begin{array}{ccc} 1 & 0 & 0\\
1 & 1 & 0\\
-1 & 0 & 1
\end{array} \right. \right] & \begin{array}{c} \\
R_{2}\rightarrow R_{3}\\
R_{3}\rightarrow R_{2}
\end{array}
\left[ \begin{array}{ccc} 1 & 0 & 1\\
0 & 1 & 1\\
0 & 2 & 3
\end{array}
\left|
\begin{array}{ccc} 1 & 0 & 0\\
-1 & 0 & 1\\
1 & 1 & 0
\end{array} \right. \right]
\end{align*}\]

Next, we make \(a_{32}=0\) in the LHS matrix by subtracting \(2R_{2}\) from \(R_{3}\). By completing this operation, we have also achieved \(a_{33}=1\) in the LHS matrix.

Finally, we make \(a_{13}=a_{23}=0\) using \(R_{3}\) as follows:

The LHS matrix is the identity matrix and so the RHS is the inverse.

\[A^{-1} = \left[\begin{array}{ccc} -2 & -1 & 2\\
-4 & -1 & 3\\
3 & 1 & -2
\end{array} \right] \]

In general, for matrices \(A\) and \(B\), \(AB\ne BA\), you should always check that \(AA^{-1}=A^{-1}A=I\).

\[\begin{align*} AA^{-1} & = \left[ \begin{array}{ccc} 1 & 0 & 1\\
-1 & 2 & 2\\
1 & 1 & 2
\end{array} \right]
\left[ \begin{array}{ccc} -2 & -1 & 2\\
-4 & -1 & 3\\
3 & 1 & -2
\end{array} \right]\\
& = \left[ \begin{array}{ccc} -2+3 & -1+1 & 2-2\\
2-8+6 & 1-2+2 & -2+6-4\\
-2-4+6 & -1-1+2 & 2+3-4
\end{array} \right]\\
& = \left[ \begin{array}{ccc} 1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{array} \right]\\
& = I
\end{align*}\] \[\begin{align*} A^{-1}A & = \left[\begin{array}{ccc} -2 & -1 & 2\\
-4 & -1 & 3\\
3 & 1 & -2
\end{array} \right]
\left[ \begin{array}{ccc} 1 & 0 & 1\\
-1 & 2 & 2\\
1 & 1 & 2
\end{array} \right]\\
& = \left[ \begin{array}{ccc} -2+1+2 & -2+2 & -2-2+4\\
-4+1+3 & -2+3 & -4-2+6\\
3-1-2 & 2-2 & 3+2-4
\end{array} \right]\\
& = \left[ \begin{array}{ccc} 1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{array} \right]\\
& = I
\end{align*}\]

Hence, \(A^{-1} = \left[ \begin{array}{ccc} -2 & -1 & 2\\
-4 & -1 & 3\\
3 & 1 & -2
\end{array} \right] \)

Your turn – finding the inverse of \(3\times3\) matrices

1. Find the inverse, if it exists, of the following matrices.
1. \(\left[ \begin{array}{ccc} 0 & 0 & -1\\
   2 & 1 & 2\\
   5 & 3 & 0
   \end{array} \right]\)
2. \(\left[ \begin{array}{ccc} 1 & 2 & 0\\
   -1 & 3 & 1\\
   2 & 5 & 2
   \end{array} \right] \)
3. \(\left[ \begin{array}{ccc} 1 & 2 & 0\\
   1 & 2 & 1\\
   1 & 2 & 4
   \end{array} \right] \)
4. \(\left[ \begin{array}{ccc} -2 & 2 & 0\\
   1 & 0 & 1\\
   1 & -1 & -2
   \end{array} \right] \)