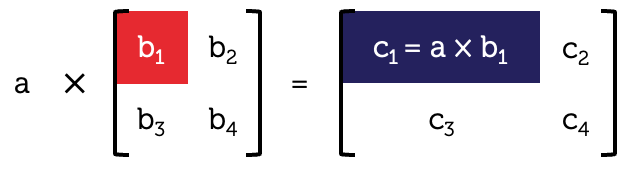Addition and subtraction of matrices
The addition and subtraction of matrices is important across many applications, from computer graphics and image processing to statistics. Use this resource to learn the rules for adding and subtracting matrices.
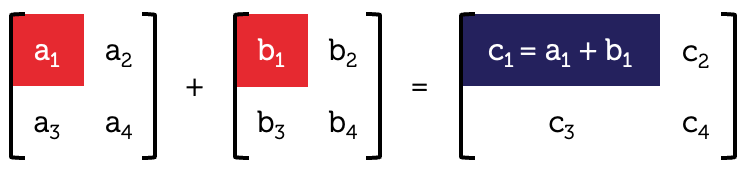
Addition of matrices
There is one key rule for adding matrices.
Matrices of the same shape (same number of rows and columns) may be added by adding the corresponding elements.
Let's consider the three matrices, \(A\), \(B\) and \(C\).
\[ A = \left[\begin{array}{ccc} 3 & 2 & -1\\
Notice that \(A\) and \(B\) are the same shape \(\left(2\times3\right)\), whereas \(C\) is \(\left(2\times2\right)\).
We can add \(A\) and \(B\) together.
\[\begin{align*} A+B & = \left[\begin{array}{ccc} 3 & 2 & -1\\
\(A+B\) is the same as \(B+A\). On the other hand, \(A+C\) and \(B+C\) are not defined as these pairs of matrices have different shapes.
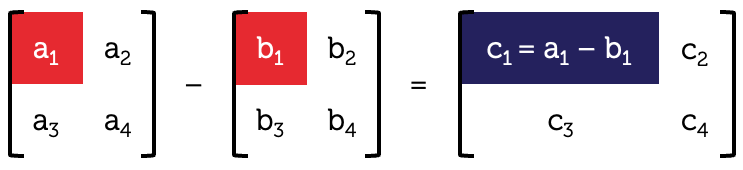
Subtraction of matrices
The rule for subtracting matrices is similar to adding them.
One matrix may be subtracted from another of the same shape by subtracting the corresponding elements.
Let's consider the same matrices \(A\), \(B\) and \(C\).
\[ A = \left[\begin{array}{ccc} 3 & 2 & -1\\
We can find \(A-B\) as they are both \(\left(2\times3\right)\) matrices.
\[\begin{align*} A-B & = \left[\begin{array}{ccc} 3 & 2 & -1\\
\(A-C\) and \(B-C\) are not defined as \(A\) and \(B\) are \(\left(2\times3\right)\) and \(C\) is \(\left(2\times2\right)\). Remember that you cannot subtract matrices that have different shapes.
We can also calculate \(B-A\).
\[\begin{align*} B-A & = \left[\begin{array}{ccc} 1 & 0 & 2\\
The order in which matrices are subtracted is important just as it is when subtracting real numbers. This means that \(A-B\neq B-A\). What you might notice, however, is that \(B-A=-\left(A-B\right)\).
Exercise – adding and subtracting matrices
Consider the matrices.
\[ A = \left[\begin{array}{c} 2\\
Find, if possible:
\(A+B\)
\(B-C\)
\(A-D\)
\(B+E\)
\(E-D\)
not possible
\(\left[ \begin{array}{cc} -4 & -1\\
not possible
\(\left[ \begin{array}{cc} 0 & 2\\
not possible
Scalar multiplication of matrices
Scalar multiplication of matrices is the same as adding the matrix by itself, multiple times.
For scalar multiplication of matrices, each element in the matrix is multiplied by the scalar (number).
Here, let's consider matrices \(D\) and \(E\).
\[ D = \left[\begin{array}{cc} 1 & 2\\
We can calculate \(5D\) which is \(5\times D\).
\[\begin{align*} 5D & = 5\times\left[ \begin{array}{cc} 1 & 2\\
Another example is \(-2D\) or \(-2\times D\).
\[\begin{align*} -2D & = -2\times\left[ \begin{array}{cc} 1 & 2\\
You can also use scalar multiplication with addition or subtraction. For example, \(5D-2E\) is \(\left(5\times D\right)-\left(2\times E\right)\).
\[\begin{align*} 5D-2E & = 5\times\left [\begin{array}{cc} 1 & 2\\
Exercise – multiplying matrices by scalars
Consider the matrices.
\(2A+B\)
\(4D-B\)
\(3C-A\)
\(B+2D+E\)
\(3C-A+3E\)
not possible
\(\left[ \begin{array}{c} 0\\
\(\left[ \begin{array}{ccc} 1 & -6 & 5\\
not possible
\(\left[ \begin{array}{ccc} 1 & -3 & 14\\
Images on this page by RMIT , licensed under CC BY-NC 4.0
Copy the iframe code above.
Go to the course in Canvas where you want to add the content.
Navigate to the page or module where you want to embed the content.
In the Rich Content Editor, click on the "HTML Editor" link.
Paste the iframe code into the HTML area.
Switch back to the Rich Content Editor to see the embedded content.
Save the changes to your page or module.
Note: Ensure that your permissions allow embedding external content in your Canvas LMS instance.