Projection of vectors

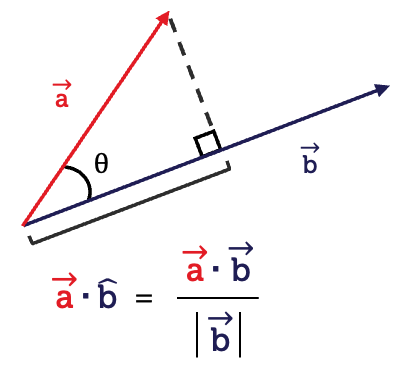
You will have learned that vectors can be resolved in two dimensions along the horizontal and vertical axes. It is also possible to resolve one vector along the line of another vector, instead of along the \(x\)- and \(y\)-axes.

Often, in physics, engineering and mathematics courses, you are asked to resolve a vector into two component vectors that are perpendicular to one another. This typically involves projecting the vector in the horizontal and vertical directions.

But, you can project a vector in any direction, not only horizontally and vertically. Here, we will look at resolving a vector in the direction of a second vector.

This is called vector projection. There are two types of vector projection:

1. scalar projection, which tells you the length of the vector pointing in a certain direction
2. vector projection, which gives you a vector that represents how much of the first vector lies in the direction of the second vector.

This will make more sense when we look at some examples.

Scalar projection

Consider the following diagram where \(\overrightarrow{PQ}=\vec{a}\) and \(\overrightarrow{PS}=\vec{b}\).

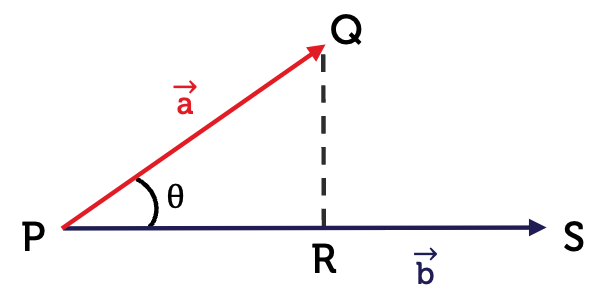
The scalar projection of the vector \(\vec{a}\) in the direction of vector \(\vec{b}\) is the length of the straight line \(PR\) or \(\left|\overrightarrow{PR}\right|\).

This forms a right-angled triangle, where:

• \(\vec{a}\) is the hypotenuse
• \(\theta\) is the angle between \(\vec{a}\) and the horizontal; and
• the scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\) is the adjacent side.

This means that the scalar projection can be calculated using:
\[\begin{align*} \cos\left(\theta\right) & = \frac{\text{adjacent}}{\text{hypotenuse}}\\
& = \frac{\left|\overrightarrow{PR}\right|}{\left|\vec{a}\right|}
\end{align*}\]

We can rearrange this to find the scalar projection:
\[\left|\overrightarrow{PR}\right| = \left|\vec{a}\right|\cos\left(\theta\right)\]

Previously, you learned how to find the angle between two vectors using a rearranged form of the scalar product equation. We can actually write the scalar projection equation in terms of this.

Remember:
\[\cos\theta=\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}\]

Substituting this into the scalar projection equation gives us:

\[\left|\overrightarrow{PR}\right|=\vec{a}\cdot\hat{b}\]

Calculating the scalar projection of vectors requires you to be able to calculate the magnitude of a vector and the scalar product. You may like to review these concepts before diving into an example.

Example – finding the scalar projection of a vector

Find the scalar projection of the vector \(\vec{a}=(2,3,1)\) in the direction of vector \(\vec{b}=(5,-2,2)\).
We need to find \(\hat{b}\) which is given by \(\dfrac{\vec{b}}{\left|\vec{b}\right|}\).
\[\begin{align*} \left|\vec{b}\right| & =\sqrt{5^{2}+(-2)^{2}+2^{2}}\\
& = \sqrt{25+4+4}\\
& = \sqrt{33}
\end{align*}\] Therefore: \[\begin{align*} \hat{b} & = \frac{\vec{b}}{\left|\vec{b}\right|}\\
& = \frac{(5,-2,2)}{\sqrt{33}}\\
& = \frac{1}{\sqrt{33}}(5,-2,2)
\end{align*}\] The scalar projection is calculated using \(\vec{a}\cdot\hat{b}\): \[\begin{align*} \vec{a}\cdot\hat{b} & = (2,3,1)\cdot\frac{(5,-2,2)}{\sqrt{33}}\\
& = \frac{\left(2\times5\right)+\left(3\times\left(-2\right)\right)+\left(1\times2\right)}{\sqrt{33}}\\
& = \frac{10-6+2}{\sqrt{33}}\\
& = \frac{6}{\sqrt{33}}
\end{align*}\]

Vector projection

The vector projection of a vector \(\vec{a}\) in the direction of vector \(\vec{b}\) is a vector pointing in the direction of \(\vec{b}\) that has the same magnitude as the straight line \(PR\) or \(\left|\overrightarrow{PR}\right|\).

You might notice that we are essentially looking at the same thing as scalar projection, but instead of finding the magnitude of the vector, we are looking at the vector itself. This gives us information about its direction.

The vector projection of \(\vec{a}\) in the direction of \(\vec{b}\) is the scalar projection multiplied by a unit vector in the direction of \(\vec{b}\).

\[\left(\vec{a}\cdot\hat{b}\right)\hat{b} = \frac{\left(\vec{a}\cdot\vec{b}\right)\vec{b}}{\left|\vec{b}\right|^{2}} \]

Example 1 – finding the vector projection of a vector

Find the vector projection of vector \(\vec{a}=(2,3,1)\) in the direction of vector \(\vec{b}=(5,-2,2)\).
Vectors \(\vec{a}\) and \(\vec{b}\) are the same as Example – finding the scalar projection of a vector, so this makes our lives easier since we already have \(\vec{a}\cdot\hat{b}\) and \(\hat{b}\).
\[\begin{align*} \left(\vec{a}\cdot\hat{b}\right)\hat{b} & = \frac{6}{\sqrt{33}}\times\frac{1}{\sqrt{33}}\left(5,-2,2\right)\\
& = \frac{6\left(5,-2,2\right)}{33}
\end{align*}\] We can also calculate this using \(\left(\vec{a}\cdot\hat{b}\right)\hat{b}=\dfrac{\left(\vec{a}\cdot\vec{b}\right)\vec{b}}{\left|\vec{b}\right|^{2}}\).
\[\begin{align*} \left(\vec{a}\cdot\hat{b}\right)\hat{b} & = \frac{\left(\vec{a}\cdot\vec{b}\right)\vec{b}}{\left|\vec{b}\right|^{2}}\\
& = \frac{\left(\left(2,3,1\right)\cdot\left(5,-2,2\right)\right)\left(5,-2,2\right)}{\left(\sqrt{33}\right)^{2}}\\
& = \frac{\left(2\times5+3\times\left(-2\right)+1\times2\right)\left(5,-2,2\right)}{33}\\
& = \frac{\left(10-6+2\right)\left(5,-2,2\right)}{33}\\
& = \frac{6\left(5,-2,2\right)}{33}
\end{align*}\]
We can further simplify this and write it in vector form:
\[\begin{align*} \frac{6\left(5,-2,2\right)}{33} & = \frac{6}{33}\left(5,-2,2\right)\\
& = \frac{2}{11}\left(5\hat{i}-2\hat{j}+2\hat{k}\right)
\end{align*}\]

Exercise – finding the scalar and vector projections of a vector

1. For \(\vec{a}=\left(2,3,1\right)\), \(\vec{b}=\left(5,0,3\right)\), \(\vec{c}=\left(0,0,3\right)\) and \(\vec{d}=\left(-2,2,-1\right)\), find:
   1. the scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\)
   2. the vector projection of \(\vec{a}\) in the direction of \(\vec{b}\)
   3. the scalar projection of \(\vec{c}\) in the direction of \(\vec{b}\)
   4. the vector projection of \(\vec{c}\) in the direction of \(\vec{a}\)
   5. the vector projection of \(\vec{d}\) in the direction of \(\vec{a}\)
   6. the vector projection of \(\vec{b}\) in the direction of \(\vec{d}\).
2. Consider \(\vec{a}=(2,0,-1)\) and \(\vec{b}=(3,5,6)\).
1. Find the scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\).
2. Describe the relationship between \(\vec{a}\) and \(\vec{b}\).

Images on this page by RMIT, licensed under CC BY-NC 4.0