Intersecting planes in 3D

Two planes in 3D can intersect. Finding this intersection has many real-life applications, including the design of buildings in architecture, 3D rendering and modelling in computer graphics, and determining paths of movement in robotics. Use this resource to learn how to determine the angle between two intersecting planes and the equation of the line of intersection.

As long as they are not parallel, two lines in 3D can intersect at a point. In the same way, two 2D planes can intersect or slice through each other given they are not parallel. The set of points where they interact forms a line. There will also be an angle between the two planes.

Angle of intersection between two planes

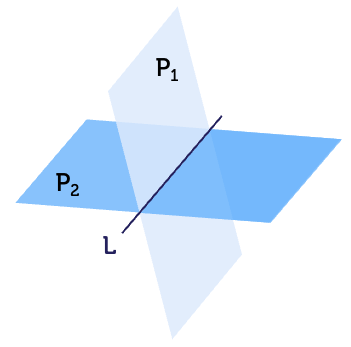
The angle between two intersecting planes is the same as the angle between the normals of the planes.

If \(N_{1}\) and \(N_{2}\) are the normals of two intersecting planes, we know that:
\[\overrightarrow{N_{1}}\cdot\overrightarrow{N_{2}} = \left| \overrightarrow{N_{1}}\right| \left|\overrightarrow{N_{2}} \right| \cos(\theta)\] where \(\theta\) is the angle between them. This follows from the definition of the scalar or dot product.

We can rearrange this to make \(\theta\) the subject:
\[\theta = \cos^{-1}\left( \frac{\overrightarrow{N_{1}}\cdot\overrightarrow{N_{2}}}{\left|\overrightarrow{N_{1}}\right|\left|\overrightarrow{N_{2}}\right|} \right) \]

In general, there are two possible angles. One is obtuse and the other is acute. Together they add up to \(180^{\circ}\).

If we want to find only the acute angle between the planes, then we just take the absolute value of the numerator:
\[\theta = \cos^{-1}\left(\frac{\left|\overrightarrow{N_{1}}\cdot\overrightarrow{N_{2}}\right|}{\left|\overrightarrow{N_{1}}\right|\left|\overrightarrow{N_{2}}\right|} \right) \]

Example – finding the angle of intersection between two planes

Find the acute angle of intersection of the planes \(x+y+z=0\) and \(x-3y+z=1\).

The plane \(x+y+z=0\) has the normal vector \(\overrightarrow{N_{1}}=\overrightarrow{i}+\overrightarrow{j}+\overrightarrow{k}\).

The plane \(x-3y+z=1\) has the normal vector \(\overrightarrow{N_{2}}=\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}\).

We can start with the numerator of the formula: \(\left| \overrightarrow{N_{1}}\cdot\overrightarrow{N_{2}} \right|\) first.
\[\begin{align*} \left| \overrightarrow{N_{1}}\cdot\overrightarrow{N_{2}} \right| & = \left|(1\times1)+(1\times(-3))+(1\times1)\right| \\
& = \left|-1\right|\\
& = 1
\end{align*}\]

Now, the denominator: \(\left| \overrightarrow{N_{1}} \right|\) and \(\left| \overrightarrow{N_{2}} \right|\).
\[\begin{align*} \left|\overrightarrow{N_{1}}\right| & =\sqrt{1^{2}+1^{2}+1^{2}}\\ & =\sqrt{3} \end{align*}\] \[\begin{align*} \left|\overrightarrow{N_{2}}\right| & =\sqrt{1^{2}+3^{2}+1^{2}}\\ & =\sqrt{11} \end{align*}\]

We can substitute these values into the formula:
\[\begin{align*} \theta & = \cos^{-1} \left(\frac{1}{\sqrt{3}\sqrt{11}} \right) \\
& = \cos^{-1} \left( \frac{\sqrt{33}}{33} \right)\\
& \approx \cos^{-1} \left( 0.1741 \right)\\
& \approx 80^{\circ}
\end{align*}\]

The angle of intersection of the two planes is approximately \(80^{\circ}\).

Exercise - finding the angle of intersection between two planes

1. Find the angle of intersection between the following planes.
1. \(x-y+z=1\) and \(2x+y-z=3\)
2. \(2x+y-z=2\) and \(3x+y-z=3\)

Line of intersection between two planes

Consider planes \(P_{1}\) and \(P_{2}\) which intersect along the line \(L\),

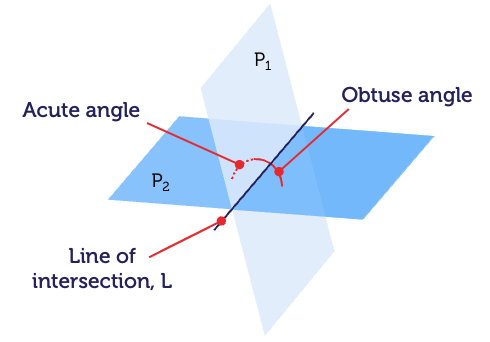
To find the equation of the line of intersection, \(L\), we solve the simultaneous equations.

Example – finding the line of intersection between two planes

Find the parametric equations for the line of intersection between \(P_{1}:\,2x+4y-z=4\) and \(P_{2}:\,x-2y+z=3\).

We have two equations but three unknowns. This means we need to introduce a parameter. We can pick any of \(x\), \(y\) or \(z\) but here, let's set \(z=t\), where \(t\in\mathbb{R}\). This would give us the equations:
\[2x+4y-t=4\] \[x-2y+t=3\]

We can multiply the second equation by \(2\) so that they become:
\[2x+4y-t=4\] \[2x-4y+2t=6\]

Adding these two equations, we can get rid of the \(x\) term:
\[\begin{align*} 2x+4y-t-2x+4y-2t & = 4-6\\
8y-3t & = -2\\
8y & = 3t-2\\
y & = \frac{3}{8}t-\frac{1}{4}
\end{align*}\]

Now that we have \(y\), we can substitute it into the second equation to find \(x\) in terms of \(t\):
\[\begin{align*} x-2\left(\frac{3}{8}t-\frac{1}{4}\right)+t & = 3\\
x-\frac{6}{8}t+\frac{2}{4}+t & = 3\\
x+\frac{1}{4}t+\frac{1}{2} & = 3\\
x & = 3-\frac{1}{4}t-\frac{1}{2}\\
x & = \frac{5}{2}-\frac{1}{4}t
\end{align*}\]

This gives us the parametric equations for the line of the intersection of the two planes:
\[x=\frac{5}{2}-\frac{1}{4}t\] \[y=\frac{3}{8}t-\frac{1}{4}\] \[z=t\] where \(t\in\mathbb{R}\).

Exercise – finding the line of intersection between two planes

Find the parametric equations for the line of intersection and the angle of intersection of the planes \(x+y+2z=0\) and \(2x-y+z=5\).

Images on this page by RMIT, licensed under CC BY-NC 4.0