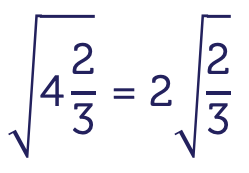I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on surds. A surd is a number that cannot be written as a fraction.
For instance numbers like root two and root seven have got a series of decimal places after the decimal point if you type those into the calculator so you can’t write those as fractions. Numbers that are not surds are written below. You can see that two can be written as a fraction two over one, one point three can be written as 13 over 10 and root four, which is two, can be written as two over one. In other words they can all be expressed as fractions.
The trick in simplifying surds is to look for square factors. Here are a number of square factors, four, which is two squared, nine, which is three squared and so on up to 100, which is 10 squared. Look at this example, we have the square root of 200 and what we do is we express it so that there’s a square factor under the square root sign which in this case is 100, shown in red, 100 times two under the square root sign is the same as the square root of 100 times the square root of two. Notice the square root of 100 is 10 so our answer is 10 root two. Notice also the square root sign is sometimes called the radical. Similarly three root 48, 48 is not a square factor but 16 times three is, which gives us three the square root of 16 times three, the root 16 is four and root three is left on its own, in other words we now have two whole numbers, three and four, which gives us 12 root three, so our answer is 12 root three.
When it comes to adding and subtracting surds one has to be mindful of the fact that only like surds can be added or subtracted. For instance, here’s a question eight root five minus three root five. The root fives are the same in both terms, in other words we can subtract these two terms, eight root five minus three root five is five root five. However, if we have this question, where we have two root three plus five root seven minus 10 root three, notice there are two different surds here, a root three and a root seven, so we have to keep those separate in our answer, so that gives us five root seven minus eight root three.
Here’s the rule for multiplying surds and it’s probably easier to illustrate this with an example. For instance root three times root two we can place both the root three and the root two under one square root sign, in other words that becomes the square root of three times two, three times two is six so the answer is root six.
A second example, we have three root five times four root seven. Three and four are the whole numbers so you multiply those two separately, whereas the root five and the root seven can go under one square root sign, the square root of five times seven, so that gives us an answer of 12 root 35.
Finally here’s another one. We start with two root 10 times seven root six, which gives us initially 14 times the square root of 10 root six, which is root 60, but when you get a large square root sign in particular see if it will simplify into something a bit smaller, in other words look for a square factor which in this case is four, in other words root 60 is the square root of four times 15. Four times root 15, the square root of, gives us two times root 15, so we now have four times two which is 28 root 15.
In dividing surds we use a similar idea and again let’s look at the example here, root 18 divided by root six is the same as the square root of 18 divided by six, which is three. In other words our answer is root three. Here’s a number four divided by a surd, root two, so here we have four, which can be expressed as root 16 divided by root two. Notice I’ve expressed both numerator and denominator as surds because we can now use the rule, which is the square root of 16 divided by two, which is root eight, and again notice that this simplifies because we can use a square factor here of four, so root four times two is two root two.
Rationalising a surd is a way of simplifying an expression where the surd is on the denominator. For instance if we have two over root five notice the surd is in the denominator here and to simplify that we can multiply two over root five by root five over root five, which is effectively one. In other words two over root five times root five over root five is two root five multiplying the top line, root five times root five is root 25 which is five. Notice the answer to root five over five has got no surd in the denominator.
Similarly here we have surds top and bottom but the purpose here is to try and get rid of the root two in the denominator, so we do as before by multiplying both top and bottom by root two over root two, which gives us root 10 on the top, root two times root two on the bottom is two times three which gives us six on the bottom. Again notice in both examples here that there are no surds in the denominator, that’s rationalising surds.
Conjugate surds are just a slight extension of the rationalising surds problem we were doing in the previous slide. Here’s an example; root three over five plus root two. What we do is we look at the denominator and then we write the conjugate of that, meaning we write the same terms five and root two but with a negative sign between them. In other words we’re multiplying by five minus root two over five minus root two. Now we multiply out the problem, this gives us root three brackets five minus root two over five plus root two multiplied by five minus root two. If we multiply out the bottom line we’ll get four terms, but notice in particular that when we multiply out this bottom line it’ll be the surds that will cancel out. In other words we’ll have no surd left in the denominator, so our answer is five root three minus root six divided by 23. Always make sure that the answer does not have a surd.
Now try some problems for yourself. The answers to these questions are on the next slide. Thanks for watching this short movie.