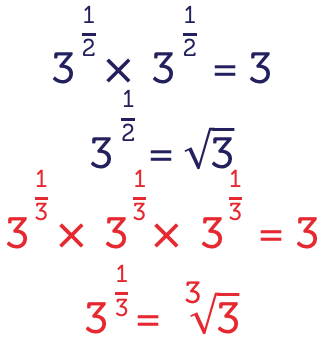Fractional indices

An index can be an integer – a counting number - either positive or negative. It can also be a fraction such as \(\dfrac{1}{2}\), \(\dfrac{3}{4}\), or \(2.5\). Use this resource to learn how the laws of indices apply to fractional indices.

Index laws

Remember the basic index laws:

1. \(a^{m}\times a^{n}=a^{m+n}\)
2. \(a^{m}\div a^{n}=a^{m-n}\)
3. \(\left(a^{m}\right)^{n}=a^{mn}\)
4. \(a^{0}=1\)
5. \(a^{-n}=\dfrac{1}{a^{n}}\)

These hold when \(m\) and \(n\) are whole numbers or fractions. From this point onwards, we will refer to them as the first index law, the second index law, and so on.

Basic fractional indices

Let's consider the fractional index, \(3^{\frac{1}{2}}\).

Using the first index law:

\[\begin{align*} 3^{\frac{1}{2}}\times3^{\frac{1}{2}} & = 3^{\frac{1}{2}+\frac{1}{2}}\\
& = 3^{1}\\
& = 3
\end{align*}\]

When \(3^{\frac{1}{2}}\) is multiplied by itself, it gives the base, \(3\). This is the same as:

\[\sqrt{3}\times\sqrt{3}=3\]

Therefore, we can say that:

\[3^{\frac{1}{2}}=\sqrt{3}\]

Now, let's consider \(2^{\frac{1}{3}}\).

Using the first index law:

\[\begin{align*} 2^{\frac{1}{3}}\times2^{\frac{1}{3}}\times2^{\frac{1}{3}} & = 2^{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}}\\
& = 2^{1}\\
& =2
\end{align*}\]

\(2^{\frac{1}{3}}\) therefore behaves like the cube root of \(2\):

\[2^{\frac{1}{3}}=\sqrt[3]{2}\]

In general, we say that \(a^{\frac{1}{n}}\) is the \(n^{\textrm{th}}\) root of \(a\). That is:
\[a^{\frac{1}{n}}=\sqrt[n]{a}\]
for any positive integer \(n\).

Example 1 – evaluating basic fractional indices

Evaluate \(4^{\frac{1}{2}}\).
\[\begin{align*} 4^{\frac{1}{2}} & = \sqrt{4}\\
& = 2
\end{align*}\]

Your turn – evaluating basic fractional indices

1. Evaluate the following expressions. If the answer is not exact, use a calculator to give a decimal approximation to two decimal places.
1. \(64^{\frac{1}{2}}\)
2. \(125^{\frac{1}{3}}\)
3. \(36^{\frac{1}{4}}\)
4. \(81^{-\frac{1}{2}}\)
5. \(128^{-\frac{1}{7}}\)
6. \(250^{\frac{1}{5}}\)

More complicated fractional indices

Consider the fraction index, \(a^{\frac{2}{3}}\).

Using the third index law:

\[\begin{align*} a^{\frac{2}{3}} & = \left(a^{2}\right)^{\frac{1}{3}}\\
& = \sqrt[3]{a^{2}}
\end{align*}\]

Since \(2\times \dfrac{1}{3}\) is the same as \(\dfrac{1}{3}\times2\), we can write:

\[\begin{align*} a^{\frac{2}{3}} & = a^{2\times\left(\frac{1}{3}\right)}\\
& = a^{\left(\frac{1}{3}\right)\times2}\\
& = \left(\sqrt[3]{a}\right)^{2}
\end{align*}\]

In general,
\[a^{\frac{p}{q}} = \sqrt[q]{a^{p}}\quad\textrm{or}\quad\left(\sqrt[q]{a}\right)^{p}\]
where \(p\) and \(q\) are integers with \(q\neq0\),

Example 1 – evaluating more complex fractional indices

Evaluate \(5^{\frac{3}{4}}\).
\[\begin{align*} 5^{\frac{3}{4}} & = \sqrt[4]{5^{3}}\\
& = \left(\sqrt[4]{5}\right)^{3}\\
& = 3.34
\end{align*}\]

Your turn – evaluating more complex fractional indices

1. Simplify the following expressions. Give your answers in index notation with positive indices.
1. \(\left(\frac{8}{27}\right)^{\frac{2}{3}}\)
2. \(\sqrt{5}\times\sqrt[3]{5}\times\sqrt[6]{5}\)
3. \(2^{\frac{5}{2}}-2^{\frac{3}{2}}\)

Images on this page by RMIT, licensed under CC BY-NC 4.0