Numbers
Use this resource to review long division.
Cubic factorisation
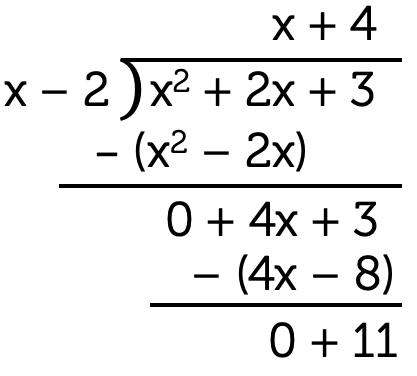
Cubic polynomials are more challenging to factorise and involve polynomial long division. This method helps break down complex polynomials into simpler components. You'll gain the ability to find factors and simplify cubic equations, which will help you solve higher-degree polynomial equations.
Polynomials
A polynomial is an algebraic expression that consists of the sum or difference of two or more algebraic terms, where the variables are raised to different powers.
Examples of polynomials are:
- \(x+7=0\)
- \(2x^{2}+9x+3=0\)
- \(7a^{2}-4=0\)
- \(n^{3}-3n+2=0\)
When a polynomial consists of two algebraic terms, it is called a binomial. When it consists of three terms, it is a trinomial, and so on.
Polynomials can also be named according to the power to which the variables are raised.
- Linear polynomials are in the form \(y=ax+b\).
- Quadratic polynomials are in the form \(y=ax^{2}+bx+c\).
- Cubic polynomials are in the form \(y=ax^{3}+bx^{2}+cx+d\).
Linear and quadratic polynomials are far simpler to factorise that cubic polynomials.
Polynomial long division
In the age of calculators, long division of numbers is not so important. However, it is still useful for factorising cubic (and higher degree) polynomials. Go back to the numbers page in arithmetic to review how to do long division.
The same algorithm (divide, multiply, subtract, bring down, repeat) is used to divide a polynomial by a polynomial of a lower degree.
To get familiar with the process, let's look at long division of a quadratic polynomial. Then, we can learn how to divide a cubic polynomial.
Example – dividing quadratic polynomials using long division
Divide \(x^{2}-5x+6\) by \(x-3\).
First, we set up the long division by writing:
\[\begin{array}{r} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \end{array}\]
Now, we can start the algorithm.
Divide the highest power of the polynomial \(x^{2}-5x+6\) by the highest power in the polynomial \(x-3\). That is, divide \(x^{2}\) by \(x\) to get \(x\). The \(x\) is placed above the \(5x\).
\[\begin{array}{r} x\phantom{)-2} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}}
\end{array}\]
Multiply \(x-3\) by \(x\) to get \(x^{2}-3x\) and write the result below the quadratic polynomial.
\[\begin{array}{r} x\phantom{)-2} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\
\underline{-~\phantom{(}(x^2-3x)\phantom{-b)}}
\end{array}\]
Subtract \(x^{2}-3x\) from \(x^{2}-5x\) to get \(-2x\).
\[\begin{array}{r} x\phantom{)-2} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\
\underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\
0\,\,\,-2x\phantom{)+6}
\end{array}\]
Bring down the \(6\).
\[\begin{array}{r} x\phantom{)-2} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}}
\\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\
0-2x+6\phantom{)}
\end{array}\]
Repeat as required until the remainder is \(0\).
Divide \(-2x\) by the leading term in \(x-3\) to get \(-2\). That is, divide \(x\) into \(-2x\) to get \(-2\) and write the \(-2\) on the top line.
\[\begin{array}{r} x-2\phantom{)} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}}
\\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\
0-2x+6\phantom{)}
\end{array}\]
Multiply \(x-3\) by \(-2\) to get \(-2x+6\) and write this below.
\[\begin{array}{r} x-2\phantom{)} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\
\underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\
0-2x+6\phantom{)} \\
\underline{~\phantom{()}(-2x+6)}
\end{array}\]
Subtract \(-2x+6\) from \(-2x+6\) to get \(0\). This is the end of the process and in this case, there is no remainder.
\[\begin{array}{r} x-2\phantom{)} \\
x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\
\underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\
0-2x+6\phantom{)} \\
\underline{-~\phantom{()}(-2x+6)} \\
0+0\phantom{)}
\end{array}\]
\(x^{2}-5x+6\) divides into \(x-3\) exactly and the answer is \(x-2\). In other words:
\[x^{2}-5x+6 = (x-3)(x-2)\]
In this particular case, it would be much easier to just factorise the quadratic or use the quadratic formula to get the same result.
However, these methods are not so helpful when the polynomials have higher degree.
Example 1 – dividing cubic polynomials using long division
Divide \(x^{3}-6x^{2}+11x-6\) by \(x-1\).
First, we set up the long division by writing:
\[\begin{array}{r} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}}
\end{array}\]
Now, we can start the algorithm.
Divide the highest power of the polynomial \(x^{3}-6x^{2}+11x-6\) by the highest power in the polynomial \(x-1\). That is, divide \(x^{3}\) by \(x\) to get \(x^{2}\). The \(x\) is placed above the \(6x^{2}\).
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}}
\end{array}\]
Multiply \(x-1\) by \(x^{2}\) to get \(x^{3}-x^{2}\) and write the result below the cubic polynomial.
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}}
\end{array}\]
Subtract \(x^{3}-x^{2}\) from \(x^{3}-6x^{2}\) to get \(-5x^{2}\).
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\
0- \, \, 5x^2\phantom{bbbi+11x)}
\end{array}\]
Bring down the \(11x\).
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\
\, \, -5x^2+11x\phantom{bbbi)}
\end{array}\]
Divide the highest power of the polynomial \(-5x^{2}+11x-6\) by the highest power in the polynomial \(x-1\). That is, divide \(-5x^{2}\) by \(x\) to get \(-5x\). The \(-5x\) is placed above the \(11x\).
\[\begin{array}{r} x^2\,\,-5x\phantom{)+6} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\
0- \, \, 5x^2+11x\phantom{bbbi)}
\end{array}\]
Multiply \(x-1\) by \(-5x\) to get \(5x^{2}+5x\) and write the result below the cubic polynomial.
\[\begin{array}{r} x^2\,-5\,x\phantom{)+6} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\
\, \, -5x^2+11x\phantom{bbbi)} \\
\underline{~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}
\end{array}\]
Subtract \(-5x^{2}+5x\) from \(-5x^{2}+11x\) to get \(6x\).
\[\begin{array}{r} x^2\,-5\,x\phantom{)+6} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}}\\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}}\\
- \, \, 5x^2+11x\phantom{bbbi)}\\
\underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\
6x \phantom{)-6}
\end{array}\]
Bring down the \(-6\).
\[\begin{array}{r} x^2\,-5\,x\phantom{)+6} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}}\\
0- \, \, 5x^2+11x\phantom{bbbi)}\\
\underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\
6x-6 \phantom{)}
\end{array}\]
Divide \(6x-6\) by the leading term in \(x-1\) to get \(6x\). That is, divide \(x\) into \(6x\) to get \(6x\) and write the \(6x\) on the top line.
\[\begin{array}{r} x^2\,-5\,x+6\phantom{)} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}}\\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}}\\
0- \, \, 5x^2+11x\phantom{bbbi)} \\
\underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\
6x-6 \phantom{)}
\end{array}\]
Multiply \(x-1\) by \(6x\) and write this below.
\[\begin{array}{r} x^2\,-5\,x+6\phantom{)} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}} \\
0- \, \, 5x^2+11x\phantom{bbbi)} \\
\underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)} \\
6x-6 \phantom{)} \\
\underline{\phantom{()}(6x-6)}
\end{array}\]
Subtract \(6x-6\) from \(6x-6\) to get \(0\). This is the end of the process and this case, there is no remainder.
\[\begin{array}{r} x^2\,-5\,x+6\phantom{)} \\
x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\
\underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}} \\
0- \, \, 5x^2+11x\phantom{bbbi)} \\
\underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\
6x-6 \phantom{)} \\
\underline{-~\phantom{()}(6x-6)} \\
0+0\phantom{)}
\end{array}\]
\(x^{3}-6x^{2}+11x-6\) divides into \(x-1\) exactly and the answer is \(x^{2}-5x+6\). In other words:
\[x^{3}-6x^{2}+11x-6=(x-1)(x^{2}-5x+6)\]
The quadratic factor can be further factorised, giving a final factorised cubic polynomial:
\[x^{3}-6x^{2}+11x-6=(x-1)(x-3)(x-2)\]
Divide \(2x^{3}-3x+1\) by \(x-1\).
The major difference from the previous example is that there is no \(x^{2}\) term in the cubic polynomial. We can rewrite it as:
\[2x^{3}-3x+1 = 2x^{3}+0x^{2}-3x+1 \]
We set up the long division by writing:
\[\begin{array}{r} x-1{\overline{\smash{\big)}\,2x^3+0x^2-3x+1\phantom{)}}}
\end{array}\]
Now, we can start the algorithm. In this example, each individual working out step is not shown.
\[\begin{array}{r} 2x^2+2x-1\phantom{)} \\
x-1{\overline{\smash{\big)}\,2x^3+0x^2-3x+1\phantom{)}}} \\
\underline{-(2x^3- 2x^2)\phantom{bbbbbbbi)}}\\
0+ \, \, 2x^2-3x\phantom{bbbi)} \\
\underline{-~\phantom{()}(2x^2-2x)}\phantom{bbb)} \\
0-\, x\,+1 \phantom{)} \\
\underline{-~\phantom{()}(-x\,+1)} \\
0\,+0\phantom{)}
\end{array}\]
\(2x^{3}-3x+1\) divides into \(x-1\) exactly and the answer is \(2x^{2}+2x-1\). In other words:
\[2x^{3}-3x+1=(x-1)(2x^{2}+2x-1)\]
Your turn – dividing polynomials using long division
- Divide the following.
- \((2x^{3}-6x^{2}+5x+2)\div (x-2)\)
- \((3x^{3}+13x^{2}+6x-12)\div (3x+4)\)
- \((3x^{3}+x-1)\div (x-1)\)
- \((x^{3}+2x-3)\div (x-1)\)
- \((2x^{4}+5x^{3}+x+3)\div (2x+1)\)
- \((2x^{3}+x^{2}+5x+12)\div (2x+3)\)
-
- \(2x^{2}-2+1\) remainder \(4\)
- \(x^{3}+3x-2\) remainder \(-4\)
- \(3x^{2}-3x+4\) remainder \(3\)
- \(x^{2}+x+3\)
- \(x^{3}_2x^{2}-x+1\) remainder \(2\)
- \(x^{2}-x+4\)
Images on this page by RMIT, licensed under CC BY-NC 4.0
