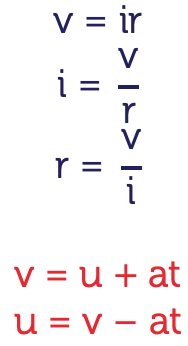Skip to main content

Transposition of formulas

The transposition of formulas involves rearranging equations to solve for a specific pronumeral or variable. You need to be able to first isolate your desired variable in order to solve problems various fields. Mastering transposition will enhance your ability to manipulate and understand mathematical relationships effectively.

Video tutorial – transposition of formulas

Watch this video to learn about the transposition of formulas.

A formula is a general rule giving the relationship between variables. The variables are represented by letters which provide us with a short hand way of writing the rule. Sometimes a formula is given in an inconvenient form and it's necessary to change the subject of the formula. When we do this we need to use certain operations, so remember the following rules; minus undoes plus, plus undoes minus, division undoes multiplication, multiplication undoes division, square root undoes square and square undoes square root.

Let's look at some examples to explain this. Let's look at the formula A plus B equals C. Now let's make A the subject, because we want to obtain A on its own we start by subtracting B so let's use the rule minus undoes plus, so we have A plus B minus B equals C minus B, so from this we obtained A equals C minus B. Note we have to use minus B on both sides of the equation, remember the saying what we do to one side of the equation we must do to the other side of the equation so we have transposed the formula to find an expression for A.

Let's look at another example. We have X minus Y equals Z and we want to make Y the subject. Notice we have a minus Y so let's use the rule plus undoes minus, we write X minus Y plus Y equals Z plus Y. Note we have used plus Y on both sides of the equation so this leaves us with X equals Z plus Y, but we want Y on its own so we use the rule minus undoes plus again to get rid of Z so we have X minus Z equals Z minus Z plus Y which leaves us with X minus Z equals Y or rewriting that with Y on the left hand side we have Y equals X minus Z.

Let's look at the formula for the area of a rectangle. The area of a rectangle is A equals L times W where A is the area, L is the length and W is the width of the rectangle. We say that A is the subject of the formula, let's say we want to find the width, W, so we use the rule division undoes multiplication by dividing both sides by L. So let's do that. We divide the left hand side by L, which is A over L and we divide the right hand side by L, so it's L times W over L. So A over L is equal to W, notice that the Ls have cancelled out on the right hand side. If we swap the left hand side and the right hand side we have W equals A divided by L.

Let's look at the formula M equals Q over P. M is the magnification of an object, Q is the size of the image and P is the size of the object. We want to find Q, the image size, so let's use the rule multiplication undoes division, so if we multiply both sides by P we get M times P equals Q over P multiplied by P and this leaves us with M times P equals Q and so if we swap both left hand side and right hand side we get Q equals M times P.

That completes the film clip of transposition of formulas. Now go to the worksheet and try some exercises for yourself. Thank you.

Formulas

Ohm's law in three formats with voltage, current and resistance the subject. The formula for constant acceleration and is final velocity is equal to initial velocity plus acceleration times time. A transposition of the previous line to make the initial velocity u the subject.

Formulas set out the mathematical relationships between variables. You may have learned that you can easily substitute numbers or values into formulas to find an unknown.

Examples include:

  • \(A=\pi r^{2}\)
  • \(s=ut+\dfrac{1}{2}at^{2}\)
  • \(S=P(1+i)^{n}\)

In these examples, \(A\), \(s\) and \(S\) are the subjects of the formulas. A subject is shown on one side of the equal sign of the formula, followed by an equal sign.

Transposing formulas

Sometimes, a formula is given in a particular form and you need to rearrange it to make a different variable the subject.

For example, you might know the area of a circle (\(A\)) and want to find the radius (\(r\)). It is perfectly reasonable to substitute the area into the formula \(A=\pi r^{2}\), but making \(r\) the subject will make problem-solving much more efficient.

To transpose formulas, we need to "undo" the operations to make a different variable the subject of the formula. You do this by doing the opposite operation. The following table tells you what you need to do to undo certain operations.

Operation Opposite operation
subtraction (\(-\)) addition (\(+\))
multiplication (\(\times\)) division (\(\div\))
square root (\(\sqrt{x}\)) square (\(x^{2}\))

Note that when taking the square root of a term—let's say, \(x^{2}\)—the answer will be \(\pm x\). This is because \(x\times x=x^{2}\) but also \((-x)\times(-x)=x^{2}\). Since we may not know whether the \(x\) is positive or negative, we must indicate that \(\sqrt{x^{2}}=\pm x\).

There is a basic rule you can follow to transpose formulas:

When rearranging equations and formulas, whatever you do on one side of the equal sign, you must do on the other.

When you encounter questions asking you to transpose a formula, you may see the terms "rearrange", "transform", "make \(x\) the subject", or "express in terms of \(x\)". These are all instructions transpose formulas.

Example 1 – transposing formulas

Make \(A\) the subject in the formula \(A+B=C\).

We need to undo the operations to get \(A\) on its own on one side of the equal sign. On the left, \(B\) is added to \(A\), so we can remove it by subtracting \(B\) on both sides.

\[\begin{align*} A+B & = C\quad\textrm{subtract \(B\) from both sides}\\
A+B-B & = C-B\\
A & = C-B
\end{align*}\]

Make \(A\) the subject in the formula \(AB=C\).

We need to undo the operations to get \(A\) on its own on one side of the equal sign. On the left, \(B\) is multiplied by \(A\), so we can remove it by dividing by \(B\) on both sides.

\[\begin{align*} AB & = C\quad\textrm{divide both sides by \(B\)}\\
\frac{AB}{B} & = \frac{C}{B}\quad\textrm{cancel out \(B\) on left}\\
A & = \frac{C}{B}
\end{align*}\]

Make \(A\) the subject in the formula \(A^{2}=B\).

We need to undo the operations to get \(A\) on its own on one side of the equal sign. On the left, \(A\) is squared, so we can remove the square by taking the square root of both sides.

\[\begin{align*} A^{2} & = B\quad\textrm{take square root of both sides}\\
\sqrt{A^{2}} & = \sqrt{B}\\
A & = \sqrt{B}
\end{align*}\]

Transform \(V=A-K\) to make \(A\) the subject.

We need to undo the operations to get \(A\) on its own on one side of the equal sign. On the right, \(K\) is subtracted from \(A\), so we can remove it by adding \(K\) to both sides.

\[\begin{align*} V & = A-K\quad\textrm{add \(K\) to both sides}\\
V+K & = A-K+K\\
V+K & = A
\end{align*}\]

We can rewrite this so that \(A\) is on the left.

\[A=V+K\]

Make \(d\) the subject of \(C=\pi d\).

We need to undo the operations to get \(d\) on its own on one side of the equal sign. On the right, \(d\) is multiplied by \(\pi\), so we can remove it by dividing by \(\pi\) on both sides.

\[\begin{align*} C & =\pi d\quad\textrm{divide by \(\pi\) on both sides}\\
\frac{C}{\pi} & = \frac{\pi d}{\pi}\quad\textrm{cancel out \(\pi\) on right}\\
\frac{C}{\pi} & = d
\end{align*}\]

We can rewrite this so that \(d\) is on the left.

\[d=\frac{C}{\pi}\]

Rearrange \(j=3w-5\) in terms of \(w\).

We need to undo the operations to get \(w\) on its own on one side of the equal sign. On the left, \(w\) is multiplied by \(3\), then \(5\) is added. To undo this, we need to work backwards and subtract the \(5\) first, then divide by \(3\).

\[\begin{align*} j & = 3w-5\quad\textrm{add \(5\) on both sides}\\
j+5 & = 3w-5+5\\
j+5 & = 3w\quad\textrm{divide by \(3\) on both sides}\\
\frac{j+5}{3} & = \frac{3w}{3}\quad\textrm{cancel out \(3\) on right}\\
\frac{j+5}{3} & = w
\end{align*}\]

We can rewrite this so that \(w\) is on the left.

\[w=\frac{j+5}{3}\]

Make \(c\) the subject of \(E=mc^{2}\).

We need to undo the operations to get \(c\) on its own on one side of the equal sign. On the left, \(c\) is squared and multiplied by \(m\). To undo this, we need to work backwards and divide by \(m\) first, then take the square root.

\[\begin{align*} E & = mc^{2}\quad\textrm{divide by \(m\) on both sides}\\
\frac{E}{m} & = c^{2}\quad\textrm{take square root of both sides}\\
\sqrt{\frac{E}{m}} & = \sqrt{c^{2}}\\
\sqrt{\frac{E}{m}} & = c
\end{align*}\]

We can rewrite this so that \(c\) is on the left.

\[c=\sqrt{\frac{E}{m}}\]

Your turn – transposing formulas

  1. Find \(n\) if \(m=n-2\).
  2. Find \(C\) if \(A=2B+C\).
  3. Find \(B\) if \(A=2B+C\).
  4. Find \(k\) if \(P=\dfrac{k}{V}\).
  5. Find \(V\) if \(PV=k\).
  6. Find \(a\) if \(v=u+at\).
  7. Find \(t\) if \(v=u+at\).
  8. Find \(A\) if \(r=\sqrt{\dfrac{A}{\pi}}\).
  9. Find \(x\) if \(A=x^{2}\).
  10. Find \(r\) if \(A=\pi r^{2}\).

  1. \(n=m+2\)
  2. \(C=A-2B\)
  3. \(B=\dfrac{A-C}{2}\)
  4. \(k=PV\)
  5. \(V=\dfrac{k}{P}\)
  6. \(a=\dfrac{v-u}{t}\)
  7. \(t=\dfrac{v-u}{a}\)
  8. \(A=\pi r^{2}\)
  9. \(x=\pm\sqrt{A}\)
  10. \(r=\pm\sqrt{\frac{A}{\pi}}\)

Images on this page by RMIT, licensed under CC BY-NC 4.0

Keywords