Factorisation
Use this resource if you need a refresher on how to identify common factors.
Algebraic fractions – Quadratics
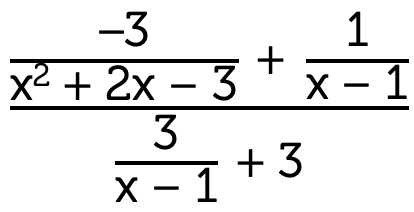
Let's take a look at algebraic fractions where the denominator is a quadratic expression. Such fractions are common in mathematics and engineering.
Before you continue with the content on this page, it is important that you are confident about identifying common factors, factorising quadratics using common factors and the difference of two squares rule.
The best way to grasp how to work with quadratics in algebraic fractions is through examples.
Example – adding or subtracting algebraic fractions with quadratics
Simplify \(\dfrac{2}{x^{2}+x-12}-\dfrac{1}{x^{2}-9}\).
You can multiply the denominators as is to form the lowest common denominator, but this would give you an \(x^{4}\). But since this can be tricky to work with, you can factorise the denominators instead.
\[\begin{align*} x^{2}+x-12 & =(x+4)(x-3)\\
x^{2}-9 & = (x+3)(x-3)
\end{align*}\]
We can rewrite the original operation as:
\[\frac{2}{x^{2}+x-12}-\frac{1}{x^{2}-9} = \frac{2}{(x+4)(x-3)}-\frac{1}{(x-3)(x+3)}\]
A common denominator is \((x+4)(x-3)(x+3)\).
To write the individual fractions with this common denominator, we need to multiply \(2\) by \((x+3)\), and \(1\) by \((x+4)\).
\[\begin{align*} & = \frac{2(x+3)}{(x+4)(x-3)(x+3)} - \frac{1(x+4)}{(x+4)(x-3)(x+3)} \\
& = \frac{2(x+3)-1(x+4)}{(x+4)(x-3)(x+3)}\\
& = \frac{2x+6-x-4}{(x+4)(x-3)(x+3)}\\
& = \frac{x+2}{(x+4)(x-3)(x+3)}\quad\textrm{where \(x\neq-4,\,-3,\,3\)}
\end{align*}\]
Your turn – adding or subtracting algebraic fractions with quadratics
Simplify \(\dfrac{2}{x^{2}+2x}+\dfrac{1}{x^{2}-4}\).
\(\dfrac{3x-4}{x(x+2)(x-2)}\quad\textrm{where \(x\neq -1,\,0,\,2\)}\)
Example – dividing algebraic fractions with quadratics
Simplify \(\dfrac{1-\frac{2}{x}}{1+\frac{2}{x}}\).
\[\begin{align*} & = \left(1-\frac{2}{x}\right)\div\left(1+\frac{2}{x}\right)\quad\textrm{convert each into single fractions}\\
& = \frac{x-2}{x} \div \frac{x+2}{x}\quad\textrm{change sign and invert last fraction}\\
& = \frac{x-2}{x} \times \frac{x}{x+2}\quad\textrm{divide top and bottom by \(1\)}\\
& = \frac{x-2}{x+2}\quad\textrm{where \(x\neq -2\)}
\end{align*}\]
& = \frac{x-2}{x} \div \frac{x+2}{x}\quad\textrm{change sign and invert last fraction}\\
& = \frac{x-2}{x} \times \frac{x}{x+2}\quad\textrm{divide top and bottom by \(1\)}\\
& = \frac{x-2}{x+2}\quad\textrm{where \(x\neq -2\)}
\end{align*}\]
Your turn – dividing algebraic fractions with quadratics
Simplify \(\dfrac{1-\frac{6}{x}}{\frac{x}{2}-3}\).
\(\dfrac{2}{x}\quad\textrm{where \(x\neq 0\)}\)
Example – simplifying algrebraic fractions with quadratics and mixed operations
Simplify \(\dfrac{\frac{-3}{x^{2}+2x-3}+\frac{1}{x-1}}{\frac{3}{x-1}+3}\).
This expression involves nested fractions. We can step through it by looking at the numerator and denominator separately.
Let's look at the numerator first. You can multiply the denominators as is to form the lowest common denominator, but this would give you an \(x^{4}\). This can be tricky to work with. Instead, you can factorise the denominators.
\[x^{2}+2x-3 = (x+3)(x-1)\]
We can rewrite the original numerator as:
\[\begin{align*} \frac{-3}{x^{2}+2x-3}+\frac{1}{x-1} & =\frac{-3}{(x+3)(x-1)}+\frac{1}{x-1}\\
& =\frac{-3}{(x+3)(x-1)}+\frac{1}{x-1}
\end{align*}\]
A common denominator is \((x+3)(x-1)\).
To write the individual fractions with this common denominator, we need to multiply \(1\) by \((x+3)\).
\[\begin{align*} & = \frac{-3}{(x+3)(x-1)} + \frac{(x+3)}{(x+3)(x-1)}\\
& = \frac{-3+x+3}{(x+3)(x-1)}\\
& = \frac{x}{(x+3)(x-1)}
\end{align*}\]
Now, we can look at the denominator. To make a common denominator, we need to multiply \(3\) by \((x-1)\).
\[\begin{align*} \frac{3}{x-1}+3 & = \frac{3}{x-1}+\frac{3(x-1)}{x-1}\\
& = \frac{3x}{x-1}
\end{align*}\]
Putting the numerator and denominator together, we get:
\[\frac{\frac{x}{(x+3)(x-1)}}{\frac{3x}{x-1}}\]
We can rewrite the fraction using a division symbol and complete the simplification.
\[\begin{align*} & = \frac{x}{(x+3)(x-1)} \div \frac{3x}{x-1}\quad\textrm{change sign and invert last fraction}\\
& = \frac{x}{(x+3)(x-1)} \times \frac{x-1}{3}\quad\textrm{divide top and bottom by \((x-1)\)}\\
& = \frac{x}{3x(x+3)}\quad\textrm{divide top and bottom by \(x\)}\\
& = \frac{1}{3(x+3)}\quad\textrm{where \(x\neq -3\)}
\end{align*}\]
& = \frac{x}{(x+3)(x-1)} \times \frac{x-1}{3}\quad\textrm{divide top and bottom by \((x-1)\)}\\
& = \frac{x}{3x(x+3)}\quad\textrm{divide top and bottom by \(x\)}\\
& = \frac{1}{3(x+3)}\quad\textrm{where \(x\neq -3\)}
\end{align*}\]
Your turn – simplifying algebraic fractions with quadratics and mixed operations
Simplify \(\dfrac{\frac{1}{x^{2}-4}+\frac{1}{2x+4}}{1+\frac{2}{x-2}}\).
\(\dfrac{1}{2(x+2)}\quad\textrm{where \(x\neq -2\)}\)
Images on this page by RMIT, licensed under CC BY-NC 4.0
