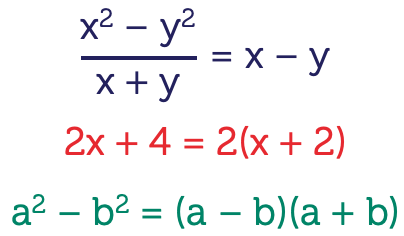Skip to main content

Algebraic fractions – Multiplication and division

Three equations. The first equation is x squared minus y squared, all divided by x plus y equals x minus y. The second equation is 2x plus 4 equations 2, brackets x plus 2, closed brackets. The third equation is a squared minus b squares equals a minus b, times a plus b.

Let's build on your understanding of basic fraction operations and algebraic expressions by looking at multiplying and dividing algebraic fractions. By mastering these skills, you'll be able to simplify and manipulate complex fractions, which is essential for solving more advanced equations and applying algebra to a variety of contexts.

Video tutorial – algebraic fractions: multiplication and division

Watch this video to learn about multiplying and dividing algebraic fractions.

Hi, this is Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on multiplying and dividing algebraic fractions. Let’s start by looking at a normal fraction, 18 over 24. Notice that 18 and 24 are divisible by six, six into 18 goes three, sixes into 24 goes four, in other words the answer is three over four. See that six is a common factor of 18 and 24. Similarly 120 over 70 has a common factor of 10 because 10 will divide into both 120 and 70 leaving us with an answer of 12 over seven.

Here’s an algebraic fraction. Notice how I’ve ... N minus N squared becomes N minus N minus N and in doing so the factor N minus N will cancel both top and bottom. Four eight squared Y over six Y squared, notice here how I’ve expanded the X squared and the Y squared to look for factors, here there’s a factor of Y top and bottom and there’s a factor of two that divides both into four and six. And finally six X plus nine Y in the denominator will actually factorise into three brackets two X plus Y three Y and in doing so the threes now become factors top and bottom.

Now let’s multiply algebraic fractions. Here’s a simple fraction where I’ve looked for factors both top and bottom, once that’s done you can cancel the factors in the numerator with factors in the denominator, as done with the previous slide. Similarly with an algebraic fraction the As will cancel because they are common factors, there’s also a factor of seven.

Here’s a more complicated algebraic fraction, but notice the method is still the same, X minus two is a factor, X is a factor and likewise with the second example, I’ve taken a factor of three out of three M plus 12 giving me three brackets M plus four, the M squared plus four M will factorise into M brackets M plus four, again notice in doing this I can now factorise the top and the bottom factors M plus four.

Dividing algebraic fractions is very much the same but remember the rule, when you divide by a fraction you change the division sign to a multiplication sign and then you invert the fraction that comes afterwards. Here I’ve done this and I’ve factored the eight and 12. Always cancel where possible.

The second example I’ve done exactly the same, the factor of four is on the top and 24 on the bottom, fours into four, fours into 24 and finally here’s another example where I’ve taken a factor of two outside of two A plus four allowing me to factorise the top and bottom of the fraction, the factor here being the A plus two.

Now try some problems for yourself. The answers to these questions are on the next slide. Thanks for watching this short movie.

Simplifying algebraic fractions

We can use the same technique to simplify algebraic fractions as we did with simplifying ordinary fractions.

Simplifying algebraic fractions may involve cancelling out common algebraic terms, as well as numbers. You can only divide the denominator and numerator if ALL the terms have a common factor.

This is the only real difference from simplifying ordinary fractions.

Example 1 – simplifying algebraic fractions

Simplify \(\dfrac{4x^{2}y}{6y^{2}}\).
\[\begin{align*} & = \frac{4x^{2}y}{6y^{2}}\quad\textrm{divide top and bottom by \(2\)}\\
& = \frac{2x^{2}y}{3y^{2}}\quad\textrm{divide top and bottom by \(y\)}\\
& = \frac{2x^{2}}{3y}
\end{align*}\]

The HCFs are \(2\) and \(y\).

Simplify \(\dfrac{a(b+2c)}{2ab}\).
\[\begin{align*} & = \frac{a(b+2c)}{2ab}\quad\textrm{divide top and bottom by \(a\)}\\
& = \frac{(b+2c)}{2b}\\
& = \frac{b+2c}{2b}
\end{align*}\]

The common factor between the numerator and denominator is \(a\). You cannot divide the \(2c\) on the top and the \(2b\) on the bottom by \(2\), since it is \(2\) is not a common factor of \(b\) in the numerator. Remember that algebraic expressions in brackets are treated together.

Simplify \(\dfrac{m-n}{(m-n)^{2}}\).
\[\begin{align*} \frac{m-n}{(m-n)^{2}} & = \frac{(m-n)(m-n)}{(m-n)(m-n)}\quad\textrm{divide top and bottom by \(m-n\)}\\
& = \frac{1}{m-n}
\end{align*}\]

Remember the special case for binomial products: \((m-n)^{2}=(m-n)(m-n)\). Since \(m\) and \(n\) are just numbers, \(m-n\) is also a number, so we can divide by \(m-n\), assuming that \(m\neq n\). This is because if \(m=n\), then \(m-n=0\) and we must not divide anything by \(0\).

Simplify \(\dfrac{3x^{2}y}{6x+9y}\).
\[\begin{align*} & = \frac{3x^{2}y}{3(2x+3y)}\quad\textrm{factorise \(3\) from bottom}\\
& = \frac{x^{2}y}{2x+3y}\quad\textrm{divide top and bottom by \(3\)}
\end{align*}\]

This example finds that \(3\) is a common factor in the denominator first. Dividing \(6x\) and \(9y\) by \(3\) gives \(2x\) and \(3y\), respectively. The \(3\) can be taken out and brackets can be written around \(2x+3y\). This process is called factorisation, which you will learn about later.

It is then clear that \(3\) is common in the numerator and denominator, and can therefore be cancelled out to simplify the fraction.

Simplify \(\dfrac{p-2}{6p-3p^{2}}\).
\[\begin{align*} & = \frac{p-2}{3p(2-p)}\quad\textrm{factorise \(3p\) from bottom}\\
& = \frac{p-2}{-3p(p-2)}\quad\textrm{factorise \(-1\) from bottom}\\
& = -\frac{1}{3p}
\end{align*}\]

Here, \(3p\) is a common factor in the algebraic terms in the denominator. Factorising it out gives \(3p(2-p)\).

Noting that the numerator is \(p-2\) and the denominator is \(2-p\), a factor of \(-1\) can be factorised out of the denominator to give \(-3p(p-2)\). This allows you to divide both the numerator and denominator by \(p-2\).

This leaves \(1\) in the numerator and \(-3p\) in the denominator. The \(-\) sign can be moved outside of the fraction, as \(-\dfrac{1}{3p}\) is the same as \(\dfrac{1}{-3}\) and \(\dfrac{-1}{3p}\).

Your turn – simplifying algebraic fractions

  1. Simplify the following fractions.
    1. \(\dfrac{12ab^{2}}{8bc}\)
    2. \(\dfrac{5x-20}{5}\)
    3. \(\dfrac{9u-18}{2u-4}\)
    4. \(\dfrac{6t-9}{12-8t}\)
    5. \(\dfrac{b}{b^{2}+7b}\)
    6. \(\dfrac{(j+4)(j-4)}{3j+12}\)
    7. \(\dfrac{2(5-v)}{3v-15}\)
    8. \(\dfrac{9r^{2}-3r}{16r-48r^{2}}\)

    1. \(\dfrac{3ab}{2c}\)
    2. \(x-4\)
    3. \(\dfrac{9}{2}\)
    4. \(-\dfrac{3}{4}\)
    5. \(\dfrac{1}{b+7}\)
    6. \(\dfrac{j-4}{3}\)
    7. \(-\dfrac{2}{3}\)
    8. \(-\dfrac{3}{16}\)

Multiplying algebraic fractions

You can also use these ideas with algebraic fractions.

When you multiply algebraic fractions, you simply multiply the numerator and denominators of the fractions.

Example 1 – multiplying algebraic fractions

\[\begin{align*} & = \frac{5a}{7}\times\frac{14}{a}\quad\textrm{divide top and bottom by \(a\)}\\
& = \frac{5}{7}\times\frac{14}{1}\quad\textrm{divide top and bottom by \(7\)}\\
& = \frac{5}{1}\times\frac{2}{1}\\
& = \frac{10}{1}\\
& = 10
\end{align*}\]

Start by dividing the \(5a\) in the top line and the \(a\) in the bottom line by a common factor \(a\). Then, divide the \(14\) in the top line and the \(7\) in the bottom line with a common factor \(7\).

The final simplified fractions can be multiplied to give \(\dfrac{10}{1}\) which is the same as \(10\).

In most of these examples, the full working is shown to step you through the thinking process. You do not need to lay your working out like this, and you may take fewer steps when you work through problems yourself.

Simplify \(\dfrac{x}{6(x-2)}\times\dfrac{3(x-2)}{x^{2}}\).
\[\begin{align*} & = \frac{x}{6(x-2)}\times\frac{3(x-2)}{x^{2}}\quad\textrm{divide top and bottom by \(x-2\)}\\
& = \frac{x}{6}\times\frac{3}{x^{2}}\quad\textrm{divide top and bottom by \(3\)}\\
& = \frac{x}{2}\times\frac{1}{x^{2}}\quad\textrm{divide top and bottom by \(x\)}\\
& = \frac{1}{2}\times\frac{1}{x}\\
& =\frac{1}{2x}
\end{align*}\]

First, we can divide the top and bottom lines by \(x-2\). Then, \(3\) is the HCF, so we can divide the numerator and denominator by \(3\). Finally, we can cancel out the \(x\)s.

The final product of the fractions would be \(\dfrac{1}{2x}\).

Simplify \(\dfrac{3m+12}{10}\times\dfrac{5}{m^{2}+4m}\).
\[\begin{align*} & = \frac{3m+12}{10}\times\frac{5}{m^{2}+4m}\quad\textrm{factorise \(3\) from top}\\
& = \frac{3(m+4)}{10}\times\frac{5}{m^{2}+4m}\quad\textrm{factorise \(m+4\) from bottom}\\
& = \frac{3(m+4)}{10}\times\frac{5}{m(m+4)}\quad\textrm{divide top and bottom by \(m+4\)}\\
& = \frac{3}{10}\times\frac{5}{m}\quad\textrm{divide top and bottom by \(5\)}\\
& = \frac{3}{2}\times\frac{1}{m}\\
& = \frac{3}{2m}
\end{align*}\]

Here, we can factorise the \(3\) out of the numerator of the first fraction. We can also factorise out the \(m\) in the denominator of the second fraction.

This allows us to cancel out the \(m+4\)s.

The highest common factor is \(5\), so we can divide the \(5\) at the top and the \(10\) at the bottom by \(5\).

Your turn – multiplying algebraic fractions

  1. Simplify the following.
    1. \(\dfrac{4a}{3}\times\dfrac{9}{a}\)
    2. \(\dfrac{32h^{2}}{9j}\times\dfrac{27j}{48h}\)
    3. \(\dfrac{3d-2}{3}\times\dfrac{4}{3d-2}\)
    4. \(\dfrac{2r+4}{3r-9}\times\dfrac{5r-15}{7r+14}\)
    5. \(\dfrac{10p-5}{3}\times\dfrac{3q+3}{2p-1}\)
    6. \(\dfrac{4g^{2}-6g}{8}\times\dfrac{3}{6g-9}\)
    7. \(\dfrac{3-2y}{33y-11}\times\dfrac{18y^{2}-6y}{7-2y}\)

    1. \(12\)
    2. \(2h\)
    3. \(\dfrac{4}{3}\)
    4. \(\dfrac{10}{21}\)
    5. \(5(q+1)\)
    6. \(\dfrac{g}{4}\)
    7. \(\dfrac{6y(3-2y)}{11(7-2y)}\)

Dividing algebraic fractions

We use the same technique for dividing algebraic fractions as we use for dividing numerical fractions.

When dividing algebraic fractions, we change the divide sign to times and invert the last fraction.

Example 1 – dividing algebraic fractions

Simplify \(\dfrac{7p}{12}\div\dfrac{3}{8}\).
\[\begin{align*} & = \frac{7p}{12}\div\frac{3}{8}\quad\textrm{change sign and invert last fraction}\\
& = \frac{7p}{12}\times\frac{8}{3}\quad\textrm{divide top and bottom by \(4\)}\\
& = \frac{7p}{3}\times\frac{2}{3}\\
& = \frac{14p}{9}
\end{align*}\]

Since dividing by a fraction is the same as multiplying by its reciprocal, we simply invert the \(\dfrac{3}{8}\) and make it a \(\dfrac{8}{3}\). The sign then changes from \(\div\) to \(\times\).

Simplify \(\dfrac{m^{2}}{n}\div6m\).
\[\begin{align*} \frac{m^{2}}{n}\div6m & =\frac{m^{2}}{n}\div\frac{6m}{1}\quad\textrm{change sign and invert last fraction}\\
& = \frac{m^{2}}{n}\times\frac{1}{6m}\quad\textrm{divide top and bottom by \(m\)}\\
& = \frac{m}{n}\times\frac{1}{6}\\
& = \frac{m}{6n}
\end{align*}\]

Remember that \(6m=\dfrac{6m}{1}\).

Simplify \(\dfrac{4(x+3)}{9}\div\dfrac{24}{5x}\).
\[\begin{align*} & = \frac{4(x+3)}{9}\div\frac{24}{5x}\quad\textrm{change sign and invert last fraction}\\
& = \frac{4(x+3)}{9}\times\frac{5x}{24}\quad\textrm{divide top and bottom by \(4\)}\\
& = \frac{(x+3)}{9}\times\frac{5x}{6}\\
& = \frac{5x(x+3)}{54}
\end{align*}\]

Simplify \(\dfrac{2a+4}{15}\div\dfrac{a+2}{6}\).
\[\begin{align*} & = \frac{2a+4}{15}\div\frac{a+2}{6}\quad\textrm{change sign and invert last fraction}\\
& = \frac{2a+4}{15}\times\frac{6}{a+2}\quad\textrm{factorise \(2\) from top}\\
& = \frac{2\left(a+2\right)}{15}\times\frac{6}{a+2}\quad\textrm{divide top and bottom by \(a+2\)}\\
& = \frac{2}{15}\times\frac{6}{1}\quad\textrm{divide top and bottom by \(3\)}\\
& = \frac{2}{5}\times\frac{2}{1}\\
& = \frac{4}{5}
\end{align*}\]

Your turn – dividing algebraic fractions

  1. Simplify the following.
    1. \(\dfrac{4m-16}{m}\div\dfrac{8m-32}{8m}\)
    2. \(\dfrac{6xy-5y^{2}}{4x+10y}\div\dfrac{12x^{2}-10xy}{12x+30y}\)

    1. \(4\)
    2. \(\dfrac{3y}{2x}\)

Images on this page by RMIT, licensed under CC BY-NC 4.0

Keywords