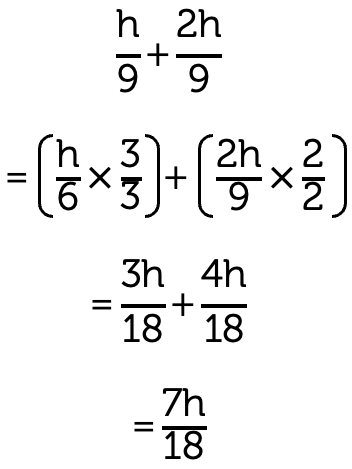Hi, this is Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on adding and subtracting algebraic fractions. Let's start by looking at a simple fraction, 18 over 24. Notice that 18 and 24 are divisible by six, six into 18 goes three, six into 24 goes four; we say that 18 and 24 have a common factor of six, so the answer is three quarters. Similarly 120 over 70 is divisible by 10, in other words 120 and 70 have a common factor of 10, that gives us an answer of 12 over seven.
Don't forget that only fractions that have a common denominator can be added or subtracted. For instance, in this case, seven tenths minus three sevenths, the common denominator here is 70, in other words 10 will divide into 70 and so will seven, so we have to carry out that process shown on the screen. At the bottom of the slide we are now subtracting these two fractions to give us an answer of 19 over 70.
Now let's move on to algebraic fractions. Again we're using the same idea as with normal fractions. Here we have H over six plus two H over nine, notice that the six and nine are different so we need a common denominator which, in this case, is 18 and thus we go through the process of adding two algebraic fractions with a common denominator of 18. Once we get to the bottom of our problem we then add the two terms up, three H plus four H which gives us seven H, notice the terms here are alike.
Here's another example, E plus one over two plus E over five, two and five must divide into a number, the common denominator here would have to be 10 so that equals E plus one over two times five over five plus E over five times two over two. Notice the next line down we have brackets, E plus one, be careful here we're multiplying five by E plus one, so it's five brackets E plus one plus two E over 10. Once we expand the brackets we get five E plus five plus two E, that gives us seven E plus five. Notice I'm adding the like terms together and there are two different terms here, an E term and a number, which is five.
Now let's look at subtracting algebraic fractions, five over two A minus three over four, so we need a common denominator, a number, that both two A and four will divide into. So four A will be that common denominator so we'd need to multiply two A by two and four by A to get our common denominator of four A. Then we have in the bottom line of our slide 10 minus three A, notice here that the terms are different so we can't do anything about them, we leave them alone, so the answer is 10 minus three A over four A.
Now try some questions for yourselves. The answers to these problems are on the next slide. Thanks for watching this short movie.