Skip to main content

Mean, mode, median

The mean, mode, and median provide a single value that is typical of the data. These measures of central tendency help summarise large datasets, making it easier to understand the overall pattern. Understanding these concepts is essential for analysing and interpreting data effectively.

Measures of central tendency

The mean, median, and mode are important tools for understanding data. They each give a single value that represents the data as a whole. These are called measures of central tendency because they show the centre or most typical values in a dataset, helping us quickly see what is common or typical.

  • The mode is the value that occurs most often. It is the value with the highest frequency (f).
  • The median is the middle value when the data is arranged in order. You can quickly find it using:
    \[\dfrac{n+1}{2}\]

    where \(n\) is the total number of data points. If the value is \(4\), the median will be the fourth value in the ordered dataset.

  • The mean or average (denoted by \(\overline{x}\)) is the sum of all the scores divided by the number of scores in the dataset:
    \[\overline{x} = \dfrac{\sum x_{n}}{n}\]

    where \(\sum x_{n}\) is the sum of each score \(x\) multiplied by its frequency (f).

Example 1 – finding the measures of central tendency

Consider the data set \(3,2,0,5,2\). Find the mode, median and mean.

To find the mode, we find the value that occurs most frequently in the dataset. The mode is \(2\) because it occurs twice.

To find the median, we need to rearrange the data so that it is ordered from smallest to largest and find the middle number:
\[0,2,\underline{2},3,5\]

The median is \(2\).

To find the mean, we use \(\overline{x}=\dfrac{\sum x_{i}}{n}\).
\[\begin{align*} \overline{x} & = \frac{\sum x_{i}}{n}\\
& = \frac{3+2+0+5+2}{5}\\
& = 2.4
\end{align*}\]

The mean is \(2.4\).

Find the mean, mode and median of the data displayed in the frequency table. The sample size \(n\) is the sum of frequencies (f): \(\sum f=8\).

\(x\) Frequency (f)
\(-3\) \(1\)
\(-1\) \(3\)
\(4\) \(1\)
\(5\) \(2\)
\(24\) \(1\)

The mode is \(-1\), which occurs \(3\) times.

When we reorder the frequencies from smallest to largest, there are \(8\) values, meaning that there are two ‘middle’ values.
\[-3,-1,-1,\underbrace{-1,4}_{\text{Middle scores}},5,5,24\]

The median is the average of these two middle values:
\[\begin{align*} \text{Median} & = \frac{-1+4}{2}\\
& = 1.5
\end{align*}\]

The mean is:
\[\frac{(-3\times1(+(-1\times3)+(4\times1)+(5\times2)+(24\times1)}{8}=4\]

Note that a disadvantage of the mean is that it is affected or distorted by extreme or outlying values.

Exercise – finding the measures of central tendency

  1. Consider the following scores: \(12,12,13,14,14,15,15,15,16\).
    1. Find the mean score.
    2. Find the median.
    3. Find the mode.
  2. Determine the mean, mode and median for the data in the frequency table.
    Score Frequency
    \(40\) \(1\)
    \(50\) \(4\)
    \(60\) \(8\)
    \(70\) \(3\)
    \(80\) \(3\)
    \(90\) \(1\)

    1. \(14\)
    2. \(14\)
    3. \(15\)
  2. Mean\(=63\), mode\(=60\) and median\(=60\)

Graphical representations of central tendency

We can visualise measures of central tendency using bell curves and stem-and-leaf plots. These tools make it easier to interpret data and understand its key characteristics.

Bell curves

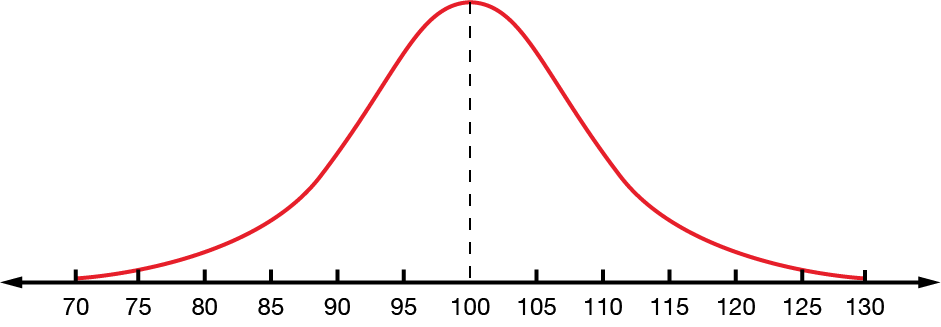
A bell curve or normal distribution graphically shows the mean in the centre with data symmetrically distributed around it. This shape highlights how values are spread out, with most clustering around the mean.

Consider this example. It is a symmetrical, bell-shaped distribution graph, where the mode, median and mean all have the same value, \(100\).

Symmetrical distribution of data

Learn more about normal distributions on this page.

Stem and leaf plots

Stem and leaf plots organise data to display the shape and distribution. They let us quickly see the median and mode, as well as the overall spread of the data.

Consider the following dataset.
\[1,1,,2,7,11,13,13,14,18,20,22,\ldots,86,94,96\]

We can organise this data in a stem and leaf plot.

  • The first row with the stem \(0\) gives us the leaf values \(1\), \(1\), \(2\) and \(7\). This just tells us that when we have \(0\) in the tens column, we have the values \(1\), \(1\), \(2\) and \(7\) in the ones column.
  • For the second row with the stem \(1\), we have all the values with a \(1\) in the tens column, so numbers ranging from \(10\) to \(19\). This would be \(11\), \(13\), \(13\), \(14\) and \(18\). The \(1\) in the tens column is written as the stem. And the leaves are the numbers in the ones columns: \(1\), \(3\), \(3\), \(4\) and \(8\).

\[\begin{array}{ccccccccccc} & 0 & \mid & & 1 & 1 & 2 & 7\\
& 1 & \mid & & 1 & 3 & 3 & 4 & 8\\
& 2 & \mid & & 0 & 2 & 3 & 7 & 9\\
& 3 & \mid & & 2 & 3 & 4 & 5 & 5 & 5 & 8\\
& 4 & \mid & & 1 & 4 & 7 & 8 & 8 & 9 & 9\\
& 5 & \mid & & 0 & 2 & 4 & 5 & 7 & 8\\
& 6 & \mid & & 1 & 4 & 5 & 6 & 9\\
& 7 & \mid & & 4 & 7 & 8\\
& 8 & \mid & & 0 & 2 & 5 & 6\\
& 9 & \mid & & 4 & 6
\end{array}\]

Cumulative count

Sometimes a stem and leaf plot will include an extra column with a cumulative count. To do this:

  1. Find the median row. This will represent the middle of the bell curve.
  2. Start at the lowest stem (first row) and count the leaves.
  3. Go to the next stem (second row) and count the leaves. Add this to the number of leaves in the first row to get a cumulative total.
  4. Move on to the next stem, count the leaves and add it to the cumulative total from the previous row. Keep adding until you reach the median.
  5. Repeat this starts from the highest stem (last row).

For the previous example, the median row has a stem of \(4\). The first stem has \(4\) leaves, so we write a \(4\) to the left of the stem. The next stem has \(5\) leaves. \(4+5=9\), so we write a \(9\) to the left of the stem. The one after that has \(5\) leaves, too. \(9+5=14\), so we write \(14\) to the left of the stem.

We continue this until we reach the stem of \(4\). The median stem does not have a cumulative total.

For the last stem, we have \(2\) leaves, so we write a \(2\) to the left of the stem. The second last stem has \(4\) leaves. \(4+2=6\) so we write the cumulative total of \(6\) to the left of the stem, and so on.

\[\begin{array}{ccccccccccccc} \mathit{4} & & \mid & 0 & \mid & & 1 & 1 & 2 & 7\\
\mathit{9} & & \mid & 1 & \mid & & 1 & 3 & 3 & 4 & 8\\
\mathit{14} & & \mid & 2 & \mid & & 0 & 2 & 3 & 7 & 9\\
\mathit{21} & & \mid & 3 & \mid & & 2 & 3 & 4 & 5 & 5 & 5 & 8\\
& & \mid & 4 & \mid & & 1 & 4 & 7 & 8 & 8 & 9 & 9\\
\mathit{20} & & \mid & 5 & \mid & & 0 & 2 & 4 & 5 & 7 & 8\\
\mathit{14} & & \mid & 6 & \mid & & 1 & 4 & 5 & 6 & 9\\
\mathit{9} & & \mid & 7 & \mid & & 4 & 7 & 8\\
\mathit{6} & & \mid & 8 & \mid & & 0 & 2 & 5 & 6\\
\mathit{2} & & \mid & 9 & \mid & & 4 & 6
\end{array}\]

Interpreting stem and leaf plots

From the stem and leaf plot, we can see that there are \(21\) scores less than or equal to \(38\) and \(20\) scores greater than or equal to \(50\). There are also \(7\) scores in the forties. This gives us \(48\) scores in total.

To find the median, we calculate \(\dfrac{n+1}{2}=\dfrac{48+1}{2}=24.5\). This means that the median value is between the \(24\)th and \(25\)th values. We know the \(21\)st score is \(38\). The median is therefore \(47.5\) (halfway between \(47\) and \(48\)).

We can also quickly see that the mode is \(35\); it occurs \(3\) times.

Exercise – interpreting graphicval representations of central tendency

Find the mode and median for the data displayed in the stem and leaf plot for which the smallest score is \(10\) and the largest \(69\).
\[\begin{array}{ccccccccccc} 1 & & \mid & & 0 & 7 & 9\\
2 & & \mid & & 1 & 1 & 3 & 4 & 6 & 7 & 8\\
3 & & \mid & & 0 & 1 & 3 & 5 & 6 & 7 & 7\\
4 & & \mid & & 0 & 1 & 1 & 1 & 2\\
5 & & \mid\\ 6 & & \mid & & 9
\end{array}\]

Mode\(=41\) and median\(=31\)

Images on this page by RMIT, licensed under CC BY-NC 4.0

Further resources

Working out a marketing budget

Explore these skills in a real world context.

Keywords