Introduction to vectors

Vectors are used to represent forces in physics, handle 2D and 3D manipulation with computer graphics, and to calculate the forces acting on materials in textiles. You also deal with vector quantities in your everyday life, from driving your car down the road to planning the shortest route to get to uni. Use this resource to gain a basic understanding of vectors.

Vectors and scalars

A vector is a measurable quantity with direction. Examples of vectors are:

• velocity – the speed at which an object is travelling in a given direction
• force – an action that causes an object to change its velocity
• displacement – the distance of an object from its original position
• acceleration – the change in speed over time.

On the other hand, a scalar quantity has magnitude only, i.e. no direction. Examples include:

• heat – the amount of thermal energy transferred or transformed within a system or between systems
• mass – the amount of matter in an object
• time – the amount of time that has passed
• volume – the amount of space occupied by a substance.

Representing vectors

Vectors are shown using an arrow that points in specific direction. The length of the line indicates the magnitude of the vector–in other words, the longer the line, the greater the magnitude. This means that a force vector of \(10\textrm{ N}\) will be \(5\) times longer than a force vector of \(2\textrm{ N}\).

Vectors in three-dimensional space are defined by three directions that are perpendicular to each other. They can be denoted as bold letters or by using a vector arrow: \(\vec{a}\) or \(\vec{b}\) or \(\vec{c}\).
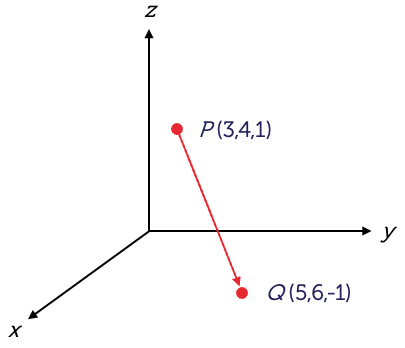
In the following figure, point P is the tail of the vector and point Q is the head of the vector. The vector is referred to as \(\overrightarrow{PQ}\), as the arrow points from point P to point Q.

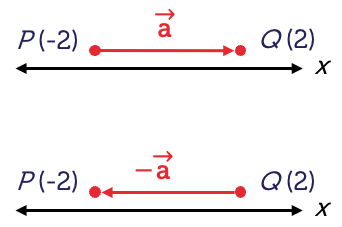
Vectors can also be defined along horizontal or vertical axes — that is, in two directions. A vector in the opposite direction from \(\vec{a}\) is denoted by \(-\vec{a}\).

Components of a vector

In the diagram, the vector \(\vec{r}\) is represented by \(\overrightarrow{OP}\) where \(P\) is the point \((x,y,z)\). This is called a position vector, which indicates where the vector is relative to the origin \(O(0,0,0)\).

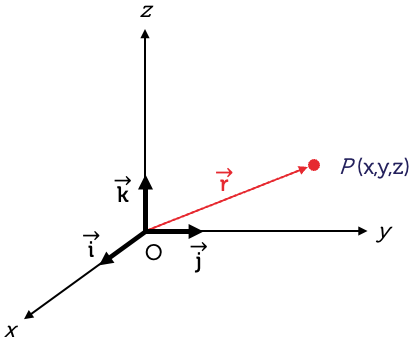
If \(\vec{i}\), \(\vec{j}\), and \(\vec{k}\) are vectors parallel to the positive directions of the \(x\)-, \(y\)- and \(z\)-axis, respectively, then:

• \(x\vec{i}\) is a vector of length \(x\) in the direction of the \(x\)-axis
• \(y\vec{i}\) is a vector of length \(y\) in the direction of the \(y\)-axis
• \(z\vec{k}\) is a vector of length \(z\) in the direction of the \(z\)-axis.

\(\overrightarrow{OP}\) is then the position vector \(x\vec{i}+y\vec{j}+z\vec{k}\), and \(x\), \(y\) and \(z\) are called the components of the vector.

The notation \((x,y,z)\) is used to denote the vector \(\vec{r}=(x\vec{i}+y\vec{j}+z\vec{k})\), as well as the coordinates of a point \(P(x,y,z)\).

Directed line segment

In the previous diagram, we defined vector \(P\) which extended from the origin O to point \(P(x,y,z)\). We can also define vectors extending from two points in space, such as from point \(P(x_{1},y_{1},z_{1})\) to point \(Q(x_{2},y_{2},z_{2})\).

\(\overrightarrow{PQ}\) is called a directed line segment or geometric vector. This vector is found by subtracting the coordinates of \(P\) (the initial point) from the coordinates of \(Q\) (the final point).

\[\overrightarrow{PQ}=(x_{2}-x_{1})\vec{i}+(y_{2}-y_{1})\vec{j}+(z_{2}-z_{1})\vec{k}\]

Let's consider the points \(P(3,4,1)\) and \(Q(5,6,-1)\).

When we apply the general formula:
\[\begin{align*} PQ & = (5-3)\vec{i}+(6-4)\vec{j}+(-1-1)\vec{k}\\
& = 2\vec{i}+2\vec{j}-2\vec{k}
\end{align*}\]

Therefore, the directed line segment \(\overrightarrow{PQ}\) is represented by the vector \(2\vec{i}+2\vec{j}-2\vec{k}\) or \((2,2,-2)\). This is also used to represent ANY directed line segment with the same length and direction as \(\overrightarrow{PQ}\).

The directed line segment \(\overrightarrow{QP}\) has the same length as \(\overrightarrow{PQ}\) but is in the opposite direction.
\[\begin{align*} \overrightarrow{QP} & = -\overrightarrow{PQ}\\
& = -(2\vec{i}+2\vec{j}-2\vec{k})\\
& = -2\vec{i}-2\vec{j}+2\vec{k}\quad\textrm{or}\quad(-2,-2,2)
\end{align*}\]

Exercise – defining directed line segments and position vectors

1. Given the points \(A(3,0,4)\), \(B(-2,4,3)\), and \(C(1,-5,0)\), find:
1. \(\overrightarrow{AB}\)
2. \(\overrightarrow{AC}\)
3. \(\overrightarrow{CB}\)
4. \(\overrightarrow{BC}\)
5. \(\overrightarrow{CA}\)
2. Look at your answers for questions b and e, and c and d. Describe what you notice.
3. Define the position vectors of the points \(A\), \(B\) and \(C\).

Adding and subtracting vectors

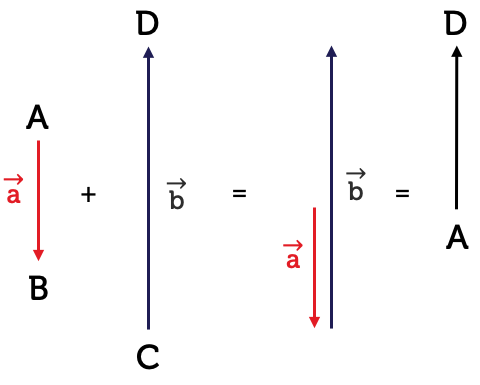
Vectors may be added or subtracted by adding or subtracting their corresponding components. For vectors pointing in the same direction, we simply place them head to tail and add them algebraically. Here, \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}\).

We can apply the same method to vectors pointing in opposite directions.

For vectors pointing in different directions, this is done graphically using the triangle law.
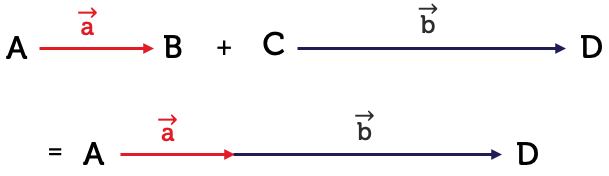
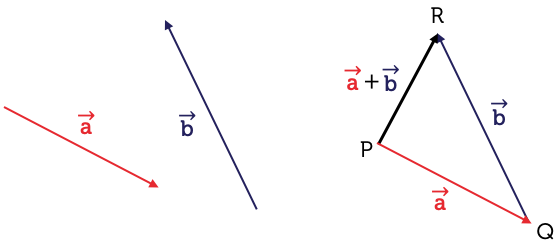
Let's consider two vectors: \(\vec{a}\) extends from point \(P\) to point \(Q\), and \(\vec{b}\) extends from point \(Q\) to point \(R\).

To add vectors \(\vec{a}\) and \(\vec{b}\), we place the tail of vector \(\vec{b}\) at the head of vector \(\vec{a}\) (point Q). The vector sum, \(\vec{a}+\vec{b}\), is the vector \(\overrightarrow{PR}\), from the tail of vector \(\vec{a}\) to the head of \(\vec{b}\).

To subtract \(\vec{b}\) from \(\vec{a}\), we reverse the direction of \(\vec{b}\) to give \(-\vec{b}\), then place them head to tail like we did with addition. \(\vec{b}\) is now extending from point \(R\) to point \(Q\).

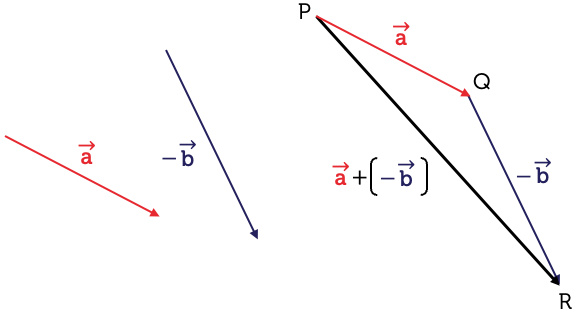
\(\vec{a}\) and \(-\vec{b}\) are added together. This means that \(\overrightarrow{PR}\) is the same as \(\vec{a}-\vec{b}\).

Example – adding and subtracting vectors

If \(\vec{a}=(-3,4,2)\) and \(\vec{b}=(-1,-2,3)\), find \(\vec{a}+\vec{b}\) and \(\vec{a}-\vec{b}\).
\[\begin{align*} \vec{a}+\vec{b} & = (-3,4,2)+(-1,-2,3)\\
& = (-3+(-1),4+(-2),2+3)\\
& = (-4,2,5)
\end{align*}\] \[\begin{align*} \vec{a}-\vec{b} & = (-3,4,2)-(-1,-2,3)\\
& = (-3-(-1),4-(-2),2-3)\\
& = (-2,6,-1)
\end{align*}\]

Exercise – adding and subtracting vectors

1. Given \(\vec{a}=(2,1,1)\), \(\vec{b}=(1,3,-3)\) and \(\vec{c}=(0,3,-2)\), find:
1. \(\vec{a}+\vec{b}\)
2. \(\vec{a}+\vec{c}\)
3. \(\vec{c}-\vec{b}\)
4. \(\vec{a}-\vec{b}\)
2. Add \(\vec{60}\) kilometres East to \(\vec{25}\) kilometres East.
3. Add \(\vec{60}\) kilometres East to \(\vec{25}\) kilometres West.
4. Add \(\vec{30}\) kilometres West to \(\vec{40}\) kilometres North.
5. Add \(\vec{30}\) kilometres West to \(\vec{30}\) kilometres South.
6. A ship sails \(\vec{40}\) kilometres North East, and then changes direction and sails \(\vec{40}\) kilometres South East. Find the displacement of the ship.
7. Two forces \(100\textrm{ N}\) North and \(100\textrm{ N}\) East are acting away from the same point. Find the sum of the vectors, or the resultant force.
8. A plane is flying due North at a speed of \(300\textrm{ km h}^{-1}\) and a Westerly wind of \(25\textrm{ km h}^{-1}\) is blowing it off course. Calculate the true speed and direction of the plane.

Magnitude of a vector

Once again, let's consider vector \(P(x,y,z)\) where \(\vec{P}=x\vec{i}+y\vec{j}+z\vec{k}\). The length or magnitude of \(\vec{P}\) is denoted by \(\left|\vec{P}\right|\) or \('\vec{P}'\), where:

\[\left|\vec{P}\right|=\sqrt{x^{2}+y^{2}+z^{2}}\]

Take, for example, the vector \(2\vec{i}+3\vec{j}-5\vec{k}\). Its length is:
\[\sqrt{2^{2}+3^{2}+(-5)^{2}}=\sqrt{38}\]

Unit vector

Any vector with a magnitude of \(1\) is called a unit vector. If \(\vec{P}\) is any vector, then a unit vector parallel to \(\vec{P}\) is written \(\hat{P}\) (read as P “hat”). The “hat” symbolises a unit vector.

The unit vector \(\hat{P}\) equals vector \(\vec{P}\) divided by its magnitude \(\left|\vec{P}\right|\).

\[\hat{P} = \frac{\vec{P}}{\left|\vec{P}\right|}\]
This can be rearranged to give:
\[\vec{P} = \left|\vec{P}\right|\hat{P}\]

The rearranged equation shows that vector \(P\) is the magnitude of the vector multiplied by its unit vector.

You should remember unit vectors \(\vec{i}\), \(\vec{j}\) and \(\vec{k}\), which are parallel to the \(x\)-, \(y\)- and \(z\)-axes, respectively. Sometimes, they are written as \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\), especially when emphasising that the vectors have a magnitude of \(1\) and point in the positive directions.

Example 1 – finding unit vectors

If \(\overrightarrow{PQ}\) is the line \(2\vec{i}-5\vec{j}+\vec{k}\), find the unit vector parallel to \(\overrightarrow{PQ}\).
To find the unit vector, divide the vector by its magnitude. Let's calculate the magnitude first.
\[\begin{align*} \overrightarrow{PQ} & = \sqrt{2^{2}+\left(-5\right)^{2}+1^{2}}\\
& = \sqrt{30}
\end{align*}\] The unit vector parallel to \(\overrightarrow{PQ}\) is therefore:
\[\begin{align*} \overrightarrow{PQ} & = \frac{\overrightarrow{PQ}}{\left|\overrightarrow{PQ}\right|}\\
& = \frac{(2\vec{i}-5\vec{j}+\vec{k})}{\sqrt{30}}\\
& = \frac{1}{\sqrt{30}}(2\vec{i}-5\vec{j}+\vec{k})
\end{align*}\]

Exercise – finding unit vectors

1. Find the length of the vectors.
1. \((3,-1,-1)\)
2. \((0,2,4)\)
3. \((0,-2,0)\)
2. Given the points \(A(3,0,4)\), \(B(0,4,3)\) and \(C(1,-5,0)\), find the unit vectors parallel to:
1. \(\overrightarrow{BA}\)
2. \(\overrightarrow{CB}\)
3. \(\overrightarrow{AC}\)

Multiplying vectors by a scalar

A scalar is a number that you multiply by to change the magnitude of a value. To multiply a vector by a scalar, \(m\), you just multiply each component by \(m\).

\[m\vec{P}=mx\vec{i}+my\vec{j}+mz\vec{k}\]

The result is a vector of length \(m\times\left|\vec{P}\right|\).

• If \(m>0\), the resultant vector is in the same direction as \(\vec{P}\).
• If \(m<0\), the resultant vector is in the opposite direction as \(\vec{P}\).

Two vectors, \(\vec{a}\) and \(\vec{b}\), are said to be parallel if and ONLY if \(\vec{a}=k\vec{b}\) where \(k\) is a real constant.

Example – multiplying vectors by a scalar

Multiply \(\vec{a}=(3\vec{i}+\vec{j}-2\vec{k})\) by \(7\) and show that \(\left|7\vec{a}\right|=7\left|\vec{a}\right|\).

To multiply by a scalar, multiply each component of the vector by the scalar.
\[\begin{align*} 7\vec{a} & = 7(3\vec{i}+\vec{j}-2\vec{k})\\
& = 21\vec{i}+7\vec{j}-14\vec{k}
\end{align*}\]

Now, let's find \(\left|7\vec{a}\right|\) and \(7\left|\vec{a}\right|\).
\[\begin{align*} \left|7\vec{a}\right| & = \sqrt{21^{2}+7^{2}+(-14)^{2}}\\
& = \sqrt{686}\\
& = \sqrt{49\times14}\\
& = 7\sqrt{14}
\end{align*}\] \[\begin{align*} \left|\vec{a}\right| & = \sqrt{3^{2}+1^{2}+(-2)^{2}}
& = \sqrt{14}\\
7\left|\vec{a}\right| & = 7\sqrt{14}
\end{align*}\]

Therefore, \(\left|7\vec{a}\right| = 7\left|\vec{a}\right| = 7\sqrt{14}\).

Exercise – multiplying vectors by a scalar.

1. Expand the following.
1. \(3(\vec{i}+3\vec{j}-5\vec{k})\)
2. \(-4(\vec{j}-3\vec{k})\)
2. If \(\vec{a}=(2,-2,1)\), \(\vec{b}=(0,1,1)\) and \(\vec{c}=(-1,3,-2)\), find:
1. \((2\vec{a}+3\vec{b})\)
2. \((3\vec{a}-2\vec{b})\)
3. \((2\vec{a}-\vec{b}+2\vec{c})\)
4. a unit vector parallel to \(2\vec{a}-\vec{b}\)
3. Identify a vector three times the length of \((6\vec{i}+2\vec{j}-5\vec{k})\) and in the opposite direction.

Images on this page by RMIT, licensed under CC BY-NC 4.0