Equation of a plane in 3D

Just as we can define an equation for a line in three dimensions, we can do the same for an entire plane–that is, we can define an equation that represents a two-dimensional space within a 3D space.

A plane is a subset of three dimensional space. You can think of it as a flat surface that extends infinitely in two directions. It may be defined as:

• the surface that goes through three points; or
• the surface containing a point and having a fixed normal vector.

Cartesian equation of a plane

A Cartesian equation is a way to describe shapes using the $x$—$y$ coordinate system. It is handy for analysing the properties and positions of geometric 2D shapes in 3D space.

Consider the following diagram, which shows a part of a plane.

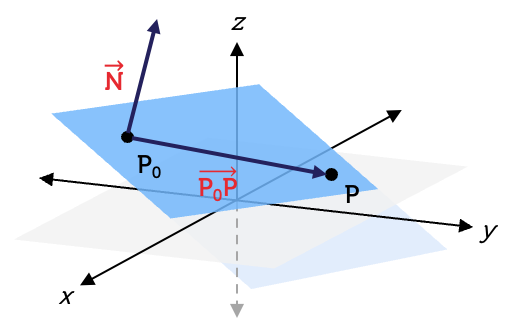
On the plane are two points, $P(x,y,z)$ and $P_0(x_0,y_0,z_0)$. The equation for the vector extending from $P_0$ to $P$ is:
$$\overrightarrow{P_{0}P}=(x-x_0)\hat{i}+(y-y_0)\hat{j}+(z-z_0)\hat{k}$$

The diagram also shows a normal vector to the plane—that is, a vector at right angles to the plane—represented by:
$$\overrightarrow{N}=a\hat{i}+b\hat{j}+c\hat{k}$$

where $a$, $b$ and $c$ are constants.
Another normal is given by $-\overrightarrow{N}=-a\hat{i}-b\hat{j}-c\hat{k}$; this just a vector in the opposite direction of $\overrightarrow{N}$ and is still at right angles to the plane.

As $\overrightarrow{N}$ is perpendicular to $\overrightarrow{P_{0}P}$, their scalar or dot product must equal $0$. Go back to the page on scalar or dot product to review this concept.

This means $\overrightarrow{N}\cdot \overrightarrow{P_{0}P}=0$. Written out in full, this is:
$$(a\hat{i}+b\hat{j}+c\hat{k})\cdot ((x-x_0)\hat{i}+(y-y_0)\hat{j}+(z-z_0)\hat{k})$$

So:

$$a(x-x_0)+b(y-y_0)+c(z-z_0)=0$$

This equation defines the plane in Cartesian coordinates.

We can rearrange the equation by expanding the brackets and moving all of the $P_0$ coordinates to one side and the $P$ coordinates to the other:
$$\begin{array}{rl}a(x-x_0)+b(y-y_0)+c(z-z_0)& =0\\ ax+by+cz& =a{x}_0+b{y}_0+c{z}_0\\ & =d\end{array}$$

where $d$ is a constant.

In fact, the general equation of a plane with the normal vector $\overrightarrow{N}=a\hat{i}+b\hat{j}+c\hat{k}$ is:

$$ax+by+cz=d$$

Some examples of equations representing planes are:

• $2x-3y+z=6$
• $x+y=4$
• $z=x-2y+3$.

Parallel planes

There are an infinite number of parallel planes that are perpendicular to a given vector. For instance $2x-3y+z=6$, $2x-3y+z=0$, $2x-3y+z=-1$ and $2x-3y+z=11$ are all perpendicular to the vector $2\hat{i}-3\hat{j}+\hat{k}$. However, only one of these will pass through a given point.

Example 1 – finding the equation of a plane

If a plane has the normal vector $\overrightarrow{N}=\hat{i}+2\hat{j}-5\hat{k}$ and contains the point $(3,4,1)$, determine the equation that represents it.

Substitute the values into the correct formula to find the equation. The normal vector is in the form $a\hat{i}+b\hat{j}+c\hat{k}$ and the point is $(x_0,y_0,z_0)$.
$$\begin{array}{rl}a(x-x_0)+b(y-y_0)+c(z-z_0)& =0\\ 1(x-3)+2(y-4)-5(z-1)& =0\\ x-3+2y-8-5z+5& =0\\ x+2y-5z& =3+8-5\\ x+2y-5z& =6\end{array}$$

You may notice that the coefficients for $\hat{i}$, $\hat{j}$ and $\hat{k}$ for the normal vector $\overrightarrow{N}$ are the same as the coefficients for $x$, $y$ and $z$ in the equation for the plane.

Exercise – finding the equation of a plane

1. Determine the vectors normal to the following planes.
1. $2x+3y+7z=13$
2. $z=x+3y-9$
2. Find the equation of the plane that contains the point $(2,3,1)$ and has the normal vector $4\hat{i}+3\hat{j}-2\hat{k}$.
3. Find the equation of the plane that contains the point $(5,-3,2)$ and has the normal vector $\hat{i}-9\hat{j}-4\hat{k}$.
4. Find the equation of the plane that contains the point $(1,-1,0)$ and is parallel to the plane $x-3y+2z=0$.
5. Find the equation of the plane that contains the points $(1,2,3)$, $(2,1,1)$ and $(-3,0,4)$.

Images on this page by RMIT, licensed under CC BY-NC 4.0