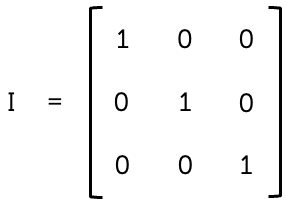Special matrices

There are a number of important special matrices to become familiar with if you are studying a STEM discipline. The transpose of a matrix is important for solving problems in structural mechanics, symmetric matrices can be applied to motion, dynamics and force calculations in physics, and orthogonal matrices have many applications in data analysis, signal processing and even medicine.

Transpose of a matrix

The transpose of a matrix \(A\) is denoted by \(A^{T}\) and is found by interchanging the rows and the columns. The first row becomes the first column, the second row becomes the second column, and so on.

If \(A\) is an \(m\times n\) matrix, then \(A^{T}\) is an \(n\times m\) matrix.

Example 1 – finding the transpose of matrices

Find the transpose of \(A= \left[ \begin{array}{cc} 1 & 2\\
3 & 4\\
5 & 6
\end{array} \right] \).
\[A^{T} = \left[ \begin{array}{ccc} 1 & 3 & 5\\
2 & 4 & 6
\end{array} \right] \]

Exercise – finding the transpose of matrices

Find the transpose of the following matrices.

1. \(A = \left[ \begin{array}{cc} 3 & -2 \end{array} \right] \)
2. \(B = \left[ \begin{array}{cc} 1 & -3\\
   -3 & 0
   \end{array} \right]\)
3. \(C = \left[ \begin{array}{ccc} 2 & 0 & 5\\
   0 & -2 & 2\\
   5 & 2 & 1
   \end{array} \right]\)

4. \(D = \left[ \begin{array}{ccc} 2 & -1 & 5\\
   5 & -1 & 2
   \end{array} \right]\)
5. \(E = \left[ \begin{array}{ccc} 0 & 1 & -1\\
   1 & 0 & 1\\
   1 & -1 & 0
   \end{array} \right]\)

Symmetric matrix

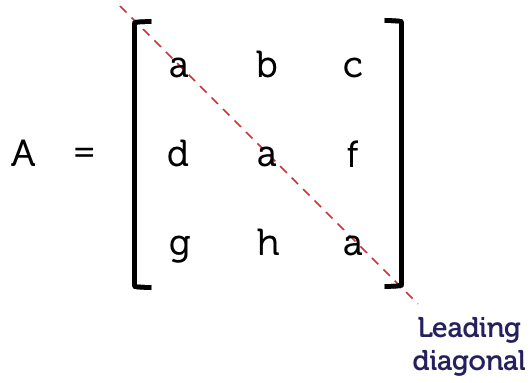
A symmetric matrix is a square matrix which is equal to its transpose. It is also symmetric about its leading diagonal (top left to bottom right).

Example 3 for finding the transpose of matrices is an example of a symmetric matrix. Let's look at some more examples.

Example 1 – determining whether matrices are symmetric

Determine whether matrix \(D\) is symmetric.
\[D = \left[ \begin{array}{cc} 1 & 3\\
3 & 4
\end{array} \right] \] \[\begin{align*} D^{T} & = \left[ \begin{array}{cc} 1 & 3\\
3 & 4\\
\end{array} \right]\\
& = D
\end{align*} \]

Therefore, \(D\) is a symmetric matrix.

Exercise – determining whether matrices are symmetric

Determine which of the following matrices are symmetric.
\[\begin{align*} A & = \left[ \begin{array}{cc} 3 & -2 \end{array} \right] \quad
B = \left[ \begin{array}{cc} 1 & -3\\
-3 & 0
\end{array} \right]\quad
C = \left[ \begin{array}{ccc} 2 & 0 & 5\\
0 & -2 & 2\\
5 & 2 & 1
\end{array} \right]\\
D & = \left[ \begin{array}{ccc} 2 & -1 & 5\\
5 & -1 & 2
\end{array} \right]\quad
E = \left[ \begin{array}{ccc} 0 & 1 & -1\\
1 & 0 & 1\\
1 & -1 & 0
\end{array} \right]
\end{align*}\]

Orthogonal matrix

A square matrix is orthogonal if \(A^{T}A=AA^{T}=I\), where \(I\) is the unit or identity matrix.

Orthogonal matrices can be further classified as rotation or reflection matrices. If the determinant of the orthogonal matrix is \(+1\), it is a rotation matrix. If the determinant is \(-1\), it is a reflection matrix.

Example – determining whether matrices are orthogonal

Determine whether matrix \(B\) is orthogonal.
\[B = \left[ \begin{array}{cc} 1 & 0\\
0 & -1
\end{array} \right] \]

To determine whether matrix \(B\) is orthogonal, we need to see whether \(BB^{T}=I\).

\[\begin{align*} B^{T} & = \left[ \begin{array}{cc} 1 & 0\\
0 & -1
\end{array} \right]\\
& = B
\end{align*}\] \[\begin{align*} BB^{T} & = \left[ \begin{array}{cc} 1 & 0\\
0 & -1
\end{array} \right]
\left[ \begin{array}{cc} 1 & 0\\
0 & -1
\end{array} \right]\\
& = \left[ \begin{array}{cc} (1\times1)+(0\times0) & (1\times0)+(0\times(-1))\\
(0\times1)+((-1)\times0) & (0\times0)+((-1)\times(-1))
\end{array} \right]\\
& = \left[ \begin{array}{cc} 1 & 0\\
0 & 1
\end{array} \right]\\
& = I
\end{align*}\]

Therefore, \(B\) is both a symmetric and orthogonal matrix.

Exercise – determining whether matrices are orthogonal

Consider the following matrices.

1. Determine which of the matrices are orthogonal.
2. Determine which of the matrices is a rotation matrix. Hint: find the determinant.