3, 4, 5 principle
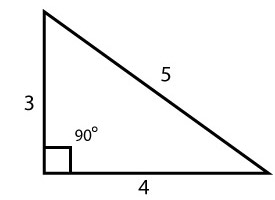
Large right angles can be constructed or checked using the 3, 4, 5 principle.
The basis of this principle is any triangle that has side lengths with a ratio 3, 4 and 5, form a 90° angle between the two shorter sides.
This principle can be used over any distance by increasing the lengths but keeping the 3, 4, 5 ratio.
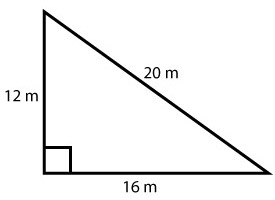
For example:
if you multiply the '3' side by 4, making it 12 m long (3 x 4 = 12 m)
then you also multiply the other two sides by 4
(4 x 4 = 16 m, and 5 x 4 = 20 m)
the sides of the triangle still have a ratio of 3, 4, 5 and so have a 90° angle.