2.1 Cannibals and Missionaries

• The Cannibals and Missionaries problem:
  Three cannibals and three missionaries come to a crocodile infested river. There is a boat on their side that can be used by either one or two persons. If cannibals outnumber the missionaries at any time, the cannibals eat the missionaries. How can they use the boat to cross the river so that all missionaries survive ?

• A state could be

    (CanLeft, MissLeft, BoatPos, CanRight, MissRight)
  
    (2, 2, RIGHT, 1, 1)
  

  ie. 2 cannibals and 2 missionaries on the left bank of the river, the boat is on the right side, together with 1 cannibal and 1 missionary.

• A legal move is one which involves moving up to two people to the opposite bank, (such that cannibals don't outnumber missionaries on either bank).

  State Space Example

• An initial state is:

    (3, 3, LEFT, 0, 0)
  

• Possible moves are:

    from (3, 3, LEFT, 0, 0) to (2, 2, RIGHT, 1, 1)
  
    from (2, 2, RIGHT, 1, 1) to (2, 3, LEFT, 1, 0)
  

• A goal state is:

    (0, 0, RIGHT, 3, 3)
  

• Note this is one of many possible representations of a state.

  Operators For M&C

  Assume the current state is:

    (cLeft, mLeft, boatPos, cRight, mRight)
  

  Move-1m1c-lr : move 1 missionary and 1 cannibal from the left bank to the right bank.

  Preconditions:

  1. boatPos = LEFT
  2. cLeft >= 1 AND mLeft >= 1
  3. (mLeft-1 >= cLeft-1) OR mLeft = 0
  4. (mRight+1 >= cRight+1) OR mRight = 0

  New State would become:

    (cLeft-1, mLeft-1, RIGHT, cRight+1, mRight+1)
  

  This operator could be applied to the state:

    (3, 3, LEFT, 0, 0)
  

  and would give the new state:

    (2, 2, RIGHT, 1, 1)
  

  This operator could not be applied to the state:

    (2, 2, RIGHT, 1, 1)
  

  Another Operator Example for M&C

  Assume the current state is:

    (cLeft, mLeft, boatPos, cRight, mRight)
  

  Move-2m-rl : move 2 missionaries from the right bank to the left bank.

  Preconditions:

  1. boatPos = RIGHT
  2. mRight >= 2
  3. cLeft <= mLeft + 2
  4. (cRight <= mRight - 2) OR mRight = 2

  New State would become:

    (cLeft, mLeft+2, LEFT, cRight, mRight-2)
  

  This operator could be applied to the state:

    (1, 1, RIGHT, 2, 2)
  

  and would give the new state:

    (1, 3, LEFT, 2, 0)
  

  This operator could not be applied to the state:

    (2, 2, RIGHT, 1, 1)
  

  Complete List of Operators for M&C

  Move-1m1c-lr
  Move-1m1c-rl
  Move-2c-lr
  Move-2c-rl
  Move-2m-lr
  Move-2m-rl
  Move-1c-lr
  Move-1c-rl
  Move-1m-lr
  Move-1m-rl
  

  As an exercise you may like to try writing down the preconditions and the output (successor) state for one or more of these operators.

  State Space Graph for M&C

• The first two levels of a directed graph for the cannibals and missionaries problem:
  
  
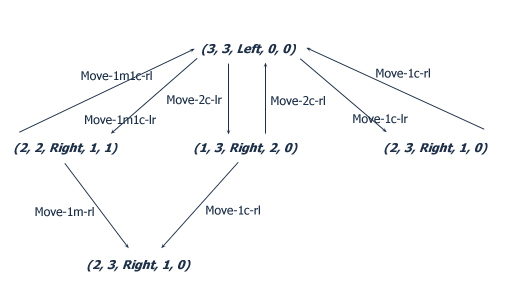
• Note that there are cycles where we return to a state we have already visited.

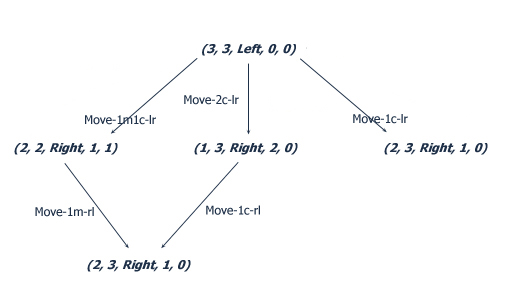
• Putting in links to nodes already visited clutters up a state-space graph.

• In coding a search we can keep a list of states already visited.

• Usually we leave out links to nodes already visited.
  

  State Space Search

• State space search involves the use of a graph to keep track of the relationships between states.

• Each node of the graph represents a state of the problem.

• Each arc in the graph represents the application of an operator in the search process.

• A state must encapsulate all the relevant information necessary to decide "what to do next", and none of the irrelevant information.
  • In the M&C problem crocodiles, (or hippos), or which way the river is flowing are not relevant.
  • Position of boat is relevant.

• The representation of states is critical when defining a problem as state space search. (Clever representations may reduce computation).

• The solution is:
  • sometimes the sequence of operators which transform the state state to the goal state
  • sometimes the actual goal state